Главные линии плоскости

Задание плоскости в пространстве и на комплексном чертеже

Комплексный чертеж плоскости

В пространстве и на комплексном чертеже (рис. 4.1) плоскость можно задать: тремя точками, не лежащими на одной прямой; прямой и не принадлежащей ей точкой; двумя пересекающимися прямыми; двумя параллельными прямыми; любой плоской фигурой; следами.

Рис. 4.1.

Следом плоскости называется линия ее пересечения с плоскостями проекций. На модели (рис. 4.2) плоскость Р пересекает плоскости проекций П₁, П₂ и П₃ по прямым линиям Р₁; P₂; P₃. Соответственно эти прямые линии называются следами плоскости Р: P₁ – горизонтальный след, P₂ – фронтальный след, P₃ – профильный след. Точки пересечения следов на осях проекций ОХ, ОУ и ОZ называются точками схода следов, соответственно Р_х, Р_у и Р_z. На рис. 4.3 показан комплексный чертёж плоскости Р, заданной следами в системе П₁/П₂/П₃.

Рис. 4.2. Рис.4.3.

4.2. Пример выполнения графической работы «Плоскости»

Даны две пересекающиеся плоскости Р и Q, заданные треугольниками АВС и SЕD. Координаты вершин треугольника АВС, принадлежащего плоскости Р, и координаты вершины S второго треугольника принадлежащего плоскости Q заданны по условию. Требуется:

1) по координатам точек вершин треугольника АВС построить его фронтальную и горизонтальную проекции;

2) определить следы 2-х прямых принадлежащих треугольнику АВС;

3) показать следы плоскости Р (Р₁,Р₂), определить координаты точки схода следов Р_Х или точки пересечения одного из следов с осью 0Z или ОY;

4) определить натуральную величину всех сторон треугольника АВС, показав владение двумя способами (прямоугольного треугольника и вращения);

5) построить на втором комплексном чертеже по координатам точек вершин два пересекающихся треугольника АВС и SЕ, их фронтальную и горизонтальную проекции, приняв за координаты точки Е – координаты точки схода следов, а за координаты точки D - значение натуральных величин сторон треугольника АВС, соответственно АВ, ВС, СА. Показать видимость сторон.

Эти задачи решаются на двух комплексных чертежах на одном листе формата АЗ.

Исходные данные

Координаты точек (мм)
S	A	B	C
10,15,0	30,60,20	10,30,58	90,20,38

Числовые данные варианта взять из приложения 11.2. Номер варианта выдается преподавателем.

Оформление данной графической работы указано в прил. 11.1.

1) Изображение построений на чертеже начинают с проработки соответствующей темы данного учебного пособия и лекционного материала.

2) В левой половине листа намечаются оси координат, по числовым значениям X и Z, X и U координат точек вершин треугольника АВС строятся его фронтальная А₂В₂С₂ и горизонтальная А₁В₁С₁ проекции. Одноименные проекции вершин соединяются прямыми линиями (рис. 4.4).

3) Определяем горизонтальные G, G₁ и фронтальные F, F₁ следы двух прямых, лежащих в плоскости треугольника АВС Известно, что следом прямой называется точка ее пересечения с плоскостью проекций. Для определения горизонтального следа прямой продолжаем фронтальную проекцию прямой А₂В₂ до пересечения с осью ОХ. в точке пересечения восстанавливаем перпендикуляр и ведем его до пересечения с продолжением горизонтальной проекции прямой А₁В₁ (рис. 4.4).

Точка пересечения является горизонтальным следом G прямой АВ, здесь же будет находиться его горизонтальная проекция G₁. а фронтальная проекция G₂ - на оси ОХ. Для определения фронтального следа прямой, продолжаем горизонтальную проекцию прямой А₁В₁ до пересечения с осью ОХ, в точке пересечения восстанавливаем перпендикуляр и ведем его до пересечения с продолжением фронтальной проекцией прямой А₂В₂. Точка пересечения является фронтальным следом F прямой АВ. здесь же будет находиться его фронтальная проекция F₂. а горизонтальная проекция F₁-на оси ОХ.

Следы второй прямой находятся аналогично.

В качестве прямых, лежащих в плоскости Р. рекомендуется брать стороны треугольника. Если вышерассмотренные построения выходят за поле чертежа, то в плоскости треугольника АВС можно взять другие устраивающие нас прямые.

Подробно данная тема рассмотрена в пункте 3.3 данного пособия

4) Для перехода к заданию плоскости Р следами Р₁ и Р₂ нужно воспользуемся найденными ранее G, G' и фронтальные F, F' следами двух прямых-, лежащих в плоскости треугольника АВС Соединяя два одноименных следа прямой, получим горизонтальный Р₁ и фронтальный Р₂ следы плоскости Р с точкой их схода Р_х. на оси ОХ.

Если точка схода следов Р_х уходит за поле чертежа, то вместо координаты точки схода следов, можно использовать координаты точек пересечения следов Р₁ и Р₂ с осямо OY и OZ (рис 4.4)

5) Натуральную величину сторон треугольника АВС можно определять методом прямоугольного треугольника. Построение на комплексном чертеже натуральной величины отрезка АС производится следующим образом (рис. 4.4): принимая горизонтальную проекцию А₁С₁ за первый катет прямоугольного треугольника, проводим через точку А₁ перпендикуляр к А₁С₁, откладываем на нем от точки А₁ отрезок А₁А', равный разности координат Z и Z' точек А и С. Полученную точку А' соединяем с точкой С₁ прямой А'С₁. Гипотенуза А'С₁ построенного прямоугольного треугольника равна натуральной величине отрезка АС.

Натуральная величина отрезка прямой может быть определена, если в качестве первого катета прямоугольного треугольника взять фронтальную проекцию отрезка (на рис 4.4 отрезок А₂В₂). Тогда второй катет должен быть равен разности координат Y концов отрезка АВ (см.рис.4.4).

Вывод: натуральная величина отрезка на комплексном чертеже строится как гипотенуза прямоугольного треугольника, первый катет которого равен одной из проекций отрезка, а второй катет равен разности расстояний от концов отрезка до той плоскости проекций, на которой взят первый катет.

Если прямоугольный треугольник построен на горизонтальной плоскости проекций П₁. то угол между проекцией отрезка и найденной его натуральной величиной будет являться углом наклона прямой к П₁ – α, если на фронтальной - к П₂ - β.

Натуральную величину сторон треугольника можно определять и методом вращения. На рис. 4.4 отрезок прямой общего положения СВ вращением вокруг оси i,перпендикулярной к плоскости П₁ и проходящей через точку B, приведен в положение, параллельное плоскости проекций П₂. Для того, чтобы отрезок СВ стал параллелен плоскости П₂, его горизонтальная проекция С₁В₁ должна стать параллельной оси ОХ, что достигается перемещением точки С₁ по дуге С₁С΄₁. Точка B неподвижна. Ее горизонтальная проекция В₁ совпадает с горизонтальной проекцией оси i (В₁≡i). Фронтальная проекция С₂ переместится вдоль прямой параллельно оси ОХ. Проведя линию связи через С₁΄, найдем в ее пересечении точку С₂΄. Соединив теперь точку В₂ и С₂΄ прямой, получим фронтальную проекцию В₂С₂΄ данного отрезка после его поворота вокруг оси i. Отрезок В₂С₂΄ равен натуральной величине ВС.

Ось вращения на чертеже не показывают. Ее можно выбирать перпендикулярно любой плоскости проекций, проводить через любой конец отрезка, вращать его по или против часовой стрелки - результат будет одинаков. При вращении отрезка вокруг оси, перпендикулярной П₂, фронтальная проекция доводится до положения, параллельного оси ОХ, а новая горизонтальная проекция даст длину отрезка.

6) В правой половине листа намечаются оси координат и по числовым значениям строят горизонтальные и фронтальные проекции треугольников ABC и SЕД. Видимость сторон пересекающихся треугольников определяют методом конкурирующих точек. Видимые отрезки сторон треугольников выделяют сплошными основными линиями, невидимые - штриховыми линиями.

7) Вопрос видимости сторон с использованием метода конкурирующих точек рассматривается подробно в подразделе 3.6 пособия.

На рис.4.4 показаны две проекции пересекающихся треугольников ABC и SЕД. На горизонтальной проекции наблюдается пересечение, образованное проекциями D₁S₁ и С₁А₁. В пересечении две конкурирующие точки К и L одна из которых принадлежит ребру CА, а другая - ребру DS. Для определения видимости от точки пересечения поднимаются в область противоположных проекций, проходят их и разворачиваются на 180 градусов, смотрят какая проекция ребра на линии проекционной связи будет ближе к наблюдателю, тогда это ребро на противоположной проекции будет видимым. В нашем случае это ребро DS. Ребро CА является невидимым, и его горизонтальная проекция изображается штриховой линией.

Аналогичным образом определяют видимость и других пересекающихся на комплексном чертеже прямых, как на фронтальной, так и на горизонтальной плоскостях проекций. В тех случаях, когда скрещивающихся ребер на чертеже нет, видимость определяется пространственным представлением.

Как полученные, так и исходные данные следует отобразить в работе в виде таблиц произвольного размера, расположенных в свободном месте поля чертежа.

4.3. Плоскость общего положения

Плоскость может занимать различные положения относительно плоскостей проекций. Плоскость, непараллельная и неперпендикулярная ни одной из плоскостей проекций, называется плоскостью общего положения. Плоскость на чертеже задают проекциями таких принадлежащих ей геометрических фигур, которые однозначно определяют ее положение в пространстве и позволяют построить любую ее точку.

На рис. 4.5 приведены модель и комплексный чертеж плоскости общего положения, заданной треугольником – Р (ΔАВС).

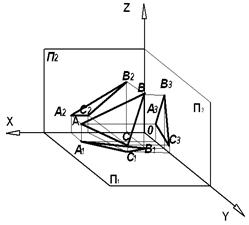
Рис. 4.5.

4.4. Принадлежность прямой и точки плоскости.

Прямая принадлежит плоскости:

а) если она проходит через две точки, принадлежащие данной плоскости (на рис. 4.6 прямая ℓ принадлежит плоскости Р (ΔАВС), т.к. имеет с ней две общие точки - 1 и 2);

б) если она проходит через точку, принадлежащую данной плоскости, и параллельна прямой, находящейся в данной плоскости (на рис. 4.7 прямая ℓ принадлежит плоскости Р (ΔАВС), т.к. имеет с ней общую точку С и парал-

Рис. 4.4. Пример выполнения графической работы «Плоскости».

лельна стороне треугольника АВ).

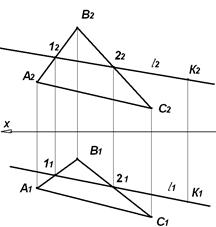
Рис. 4.6. Рис. 4.7.

Если плоскость задана следами, то прямая принадлежит плоскости:

а) если следы прямой находятся на одноимённых следах плоскости (рис. 4.8);

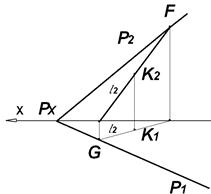
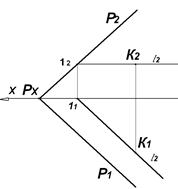
Рис. 4.8. Рис. 4.9.

б) если она параллельна одному из следов плоскости и имеет с другим общую точку (рис. 4.9).

Точка принадлежит плоскости, если она принадлежит прямой, лежащей в заданной плоскости. Следовательно, для построения такой точки, принадлежащей заданной плоскости, нужно построить вначале в этой плоскости прямую, а затем на ней взять точку (например точка К на рис. 4.6, 4.7, 4.8, 4.9).

Прямые, принадлежащие плоскости и в то же время параллельные горизонтальной, фронтальной или профильной плоскости проекций, называются главными линиями плоскости (рис. 4.10).

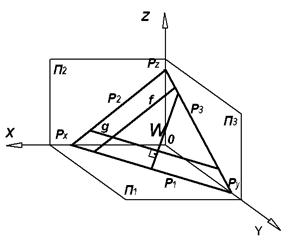
Рис. 4.10. Рис. 4.11.

Построение горизонтали g (рис. 4.11), принадлежащей плоскости Р (ΔАВС), начинают с проведения ее фронтальной проекции g₂ параллельно оси ОX, а горизонтальную проекцию g₁ проводят по построению из условия принадлежности данной плоскости.

Построение фронтали f, принадлежащей плоскости, начинают с проведения ее горизонтальной проекции f₁ параллельно оси OX, а фронтальную проекцию f₂ получают построением, исходя также из условия принадлежности.

Аналогично строятся проекции главных линий плоскости, если плоскость задана следами (рис. 4.12).

Рис. 4.12. Рис. 4.13.

Прямые, принадлежащие плоскости и перпендикулярные горизонталям, фронталям или профильным прямым этой плоскости, называются линиями наибольшего наклона или ската.

Например, прямая w является линией наибольшего наклона данной плоскости Р к горизонтальной плоскости проекций П₁ (рис. 4.10). На рис. 4.13 представлен комплексный чертеж линии наибольшего наклона w плоскости Р (ΔАВС) к плоскости проекций П₁.

Построение линии наибольшего ската w начинают с проведения ее горизонтальной проекции w ₁ перпендикулярно горизонтальной проекции горизонтали g₁,основываясь на свойстве проецирования прямого угла без искажения. Фронтальную проекцию w₂ получают построением, исходя из условия принадлежности прямой w плоскости Р (ΔАВС).

Величину угла a наклона линии наибольшего ската w, а, следовательно, и самой плоскости к горизонтальной плоскости проекций П₁ можно определить способом прямоугольного треугольника.

Дата добавления: 2014-01-05