Пересечение двух плоскостей

Две плоскости пресекаются по прямой линии, общей для обеих плоскостей. Положение прямой линии определяется положением двух принадлежащих ей точек. Следовательно, для построения линии пересечения двух плоскостей достаточно определить две точки, общие для обеих заданных плоскостей.

Если плоскости Р и Q заданы следами (рис.4.50), то проще отметить точки M и N, являющиеся точками пересечения их одноименных следов. Тогда M₁N₁ и M₂N₂ будут являться, соответственно, горизонтальной и фронтальной проекциями линии пересечения MN плоскостей P и Q.

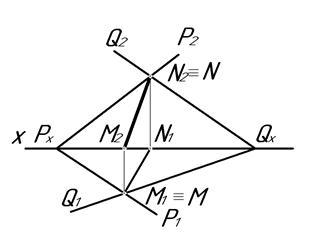
Рис. 4.50.

Приведём примеры построения линии пересечения (МN) двух плоскостей, заданных следами, когда одна из них или обе являются плоскостями частного положения.

На рис. 4.51 показан комплексный чертеж пересечения плоскости Р общего положения с плоскостью Q горизонтально проецирующего положения - P(P₁;P₂) ∩ (Q₁;Q₂), линия их пересечения ℓ [ MN ] является прямой общего положения.

На рис. 4.52 показан комплексный чертеж пересечения плоскости Р общего положения с плоскостью Q горизонтального уровня - P(P₁;P₂) ∩ (Q₁;Q₂), линия их пересечения ℓ является прямой горизонтального уровня.

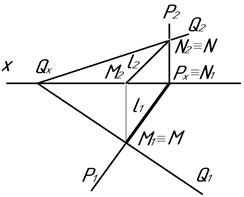
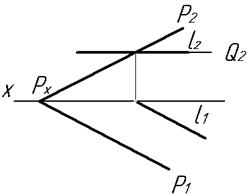
Рис. 4.51. Рис. 4.52.

На рис. 4.53 показан комплексный чертеж пересечения плоскости Р горизонтально проецирующего положения с плоскостью Q горизонтального уровня - P(P₁;P₂) ∩ (Q₁;Q₂), линия их пересечения ℓ является прямой горизонтального уровня.

На рис. 4.54 показан комплексный чертеж пересечения плоскостей Р и Q одинакового горизонтально проецирующего положения - P(P₁;P₂) ∩ (Q₁;Q₂), следовательно и линия их пересечения ℓ будет занимать такое же горизонтально проецирующее положение.

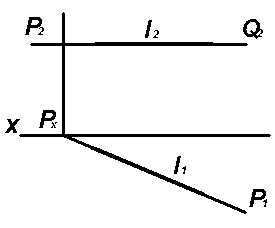
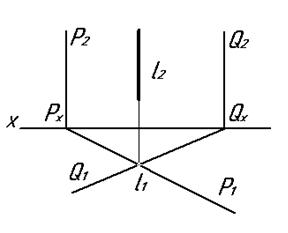
Рис. 4.53. Рис. 4.54.

Если же пересекающиеся плоскости (или одна из них) заданы не следами, то для построения их линии пересечения применяется метод вспомогательных секущих плоскостей.

Сущность этого метода состоит в том, что обе заданные плоскости (рис. 4.55), например Р(ΔАВС) и Q(ΔSDE) пересекаются третьей R (где R₂ - фронтальный след вспомогательной секущей плоскости частного положения - горизонтального уровня). Затем строятся линии пересечения первой заданной плоскости с третьей (1А), второй заданной плоскости с третьей (2Е). Там, где эти линии пресекаются, и будет находиться общая точка М заданных плоскостей. При введении еще одной вспомогательной секущей плоскости находиться вторая общая точка. В рассмотренном выше примере вторая общая точка уже есть, т.к. С º D (С₁ºD₁,С₂ºD₂), следовательно проведенные ℓ₁ и ℓ₂ являются горизонтальной и фронтальной проекциями линии пересечения двух плоскостей.

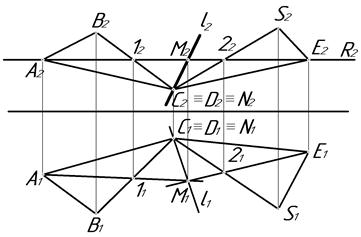
Рис. 4.55.

Метод вспомогательных секущих плоскостей может быть применён для построения линии пересечения двух плоскостей и в том случае, если пересекающиеся плоскости заданы следами, но одна пара их следов или обе в пределах чертежа не пересекается (рис. 4.56).

Рис. 4.56.

Дата добавления: 2014-01-05