Многогранные поверхности пересекаются друг с другом в общем случае по пространственным замкнутым ломаным линиям, которые в частных случаях могут оказаться плоскими

Рассмотрим построение линии пересечения многогранников, двух кривых поверхностей (поверхностей вращения), многогранных и кривых поверхностей.

Взаимное пересечение поверхностей

Форма большинства сложных деталей механизмов и машин образована сочетанием элементарных поверхностей, пересекающихся друг с другом. Поэтому, при составлении технических чертежей, необходимо уметь строить проекции линий, по которым пересекаются эти поверхности.

Две поверхности пересекаются по линии или их совокупности, которая одновременно принадлежит каждой из них. Поэтому еще ее называют линией перехода одной поверхности в другую.

Общий прием построения линии пересечения поверхностей будет иметь алгоритм:

1. Выбирается вид вспомогательных поверхностей

2. Строятся линии пересечения вспомогательных поверхностей с заданными поверхностями.

3. Находятся точки пересечения построенных линий, которые затем соединяют между собой.

Выбор вида и положения вспомогательных поверхностей определяется в основном тремя соображениями:

1. Необходимостью определения положения ряда опорных точек линии пересечения.

2. Вспомогательные поверхности должны пересекать каждую из заданных поверхностей по линиям, которые проецируются в графически простые линии – прямые, окружности.

3. Вспомогательные поверхности должны пересекать заданные поверхности в пределах зоны возможного расположения линии пересечения, чтобы избежать лишних построений.

10.2.1. Взаимное пересечение многогранников

При решении задач определяют вершины ломанной (опорные точки линии пересечения), а затем соединяют - отрезками прямых те пары вершин, которые принадлежат одной и той же грани первого многогранника и одновременно одной и той же грани второго многогранника.

Покажем построение линии пересечения прямой четырехугольной призмы АBСD и трехгранной пирамиды SEFТ (рис. 10.2). Призма своим основанием стоит на горизонтальной плоскости проекций. Горизонтальные проекции ее вертикальных ребер преобразуются в точки, а грани боковой поверхности представляют собой горизонтально проецирующие плоскости. Линия их пересечения проходит через точки 1, 2, 3, 4, 5, 6 пересечения ребер пирамиды с гранями призмы и точки 9, 10 пересечения ребра призмы А с гранями пирамиды SFE и STE. При определении точек 9, 10 через ребро А и вершину S пирамиды проводили вспомогательную плоскость Р (где Р₁ ее горизонтальный след) горизонтально проецирующего положения. Плоскость Р пересекает пирамиду по прямым S7 и S8 с которыми в точках 9 и 10 пересекается ребро А. Соединяя каждые пары точек одних и тех же граней отрезками прямых, получили две линии пересечения многогранников – треугольник 1-2-3 и пространственный многоугольник 4-5-6-9-10.

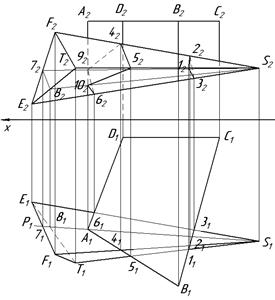
Рис. 10.2.

10.2.2. Взаимное пересечение кривых поверхностей

Линия пересечения двух кривых поверхностей в общем случае представляет собой пространственную кривую, которая может распадаться на две и более частей (случай проницания). Точки этой линии (опорные и промежуточные) определяются при помощи основного способа построения линии пересечения поверхностей.

Покажем построение линии пересечения прямого кругового конуса и сферы (рис. 10.3). Характерные точки 1 и 2, являющиеся, соответственно высшей и низшей точками линии пересечения, построены с помощью вспомогательной секущей плоскости Q фронтального уровня, проведенной через ось конуса и центр сферы.

Для нахождения проекций точек 3, 4 и 5, 6 проводили вспомогательные секущие плоскости горизонтального уровня. Причем одна из них (Р) проведена через центр сферы, благодаря чему получены горизонтальные проекции 3₁, 4₁, а затем поднимаясь по ЛПС до места введения вспомогательной секущей плоскости и фронтальные проекции 3₂, 4₂ характерных точек 3 и 4, определяющих границу видимости линии пересечения на горизонтальной плоскости проекций П₁.

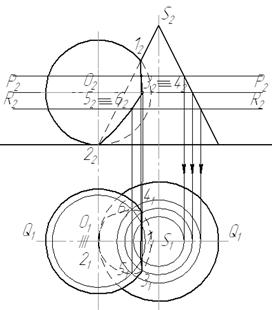
Рис. 10.3.

10.2.3. Взаимное пересечение кривых и многогранных поверхностей

Кривая и многогранная поверхности пересекаются по составной кривой, состоящей из нескольких плоских кривых, каждая из которых - результат пересечения граней многогранной поверхности с кривой поверхностью, а точки излома – точки встречи ребер многогранника с кривой поверхностью. В случае проницания эта составная кривая распадается на две части и более.

Покажем построение на комплексном чертеже линии пересечения поверхностей прямого кругового конуса и трехгранной призмы (рис. 10.4).

Рассмотрев условие задачи, можно представить, что нижняя грань призмы пересекает поверхность конуса по дуге окружности, которая будет проецироваться на горизонтальную плоскость проекций в дугу окружности, на профильную плоскость проекций – в виде отрезка прямой, частично совпадающим с профильной проекцией нижней грани призмы, и на фронтальную плоскость проекций – в виде отрезка прямой, полностью совпадающим с фронтальной проекцией нижней грани призмы. Боковые грани призмы пересекают поверхность конуса по параболическим кривым, которые на горизонтальную и профильную плоскости проекций будут проецироваться в виде частей параболы, а на фронтальную плоскость проекций – в виде отрезков прямых, полностью совпадающих с фронтальной проекцией боковых граней призмы.

Рис. 10.4.

Для построения опорных точек 1 и 2 (самая верхняя и самая нижняя), принадлежащих линии пересечения призмы и конуса, проведена вспомогательная плоскость Р профильного уровня (где Р₁ - ее горизонтальный след). Плоскость Р пересекает конус и призму по прямым, профильные проекции которых совпадают с очерковыми пересекающихся поверхностей (треугольник и прямоугольник). В пересечении этих очерковых отмечены профильные проекции точек 1 и 2. Горизонтальные и фронтальные проекции точек 1 и 2 определены по линиям проекционной связи, проведенных до линии введения вспомогательной секущей плоскости Р.

Для построения опорных точек 3 и 4 (самая левая и самая правая), принадлежащих линии пересечения призмы и конуса, проведена через нижнюю грань призмы вспомогательная плоскость Q горизонтального уровня (где Q₂ – ее фронтальный след). В пересечении плоскости Q с конусом и призмой получены соответственно сечения – окружность и прямоугольник, пересечение которых на горизонтальной плоскости проекций дает положение точек 3₁ и 4₁. Фронтальные и профильные проекции точек 3 и 4 определены по линиям проекционной связи, проведенных до линии введения вспомогательной секущей плоскости Q.

Для построения проекций промежуточных точек 5 и 6, принадлежащих линии пересечения призмы и конуса, проведена вспомогательная плоскость R горизонтального уровня (где R₂ – ее фронтальный след). В пересечении плоскости R с конусом и призмой получены соответственно сечения – окружность и прямоугольник (меньших размеров, чем при введении плоскости Q), пересечение которых на горизонтальной плоскости проекций дает положение точек 5₁ и 6₁. Фронтальные и профильные проекции точек 5 и 6 определены по линиям проекционной связи, проведенных до линии введения вспомогательной секущей плоскости R.

Рассмотренная выше задача может быть решена еще проще, так как одна из пересекающихся поверхностей (призма) занимает проецирующее положение к фронтальной плоскости проекций П₂. Следовательно, линия пересечения прямого кругового конуса и трехгранной призмы совпадает с фронтальной проекцией призмы. И тогда решение задачи сведется к построению недостающих горизонтальных и профильных проекций точек линии пересечения на одной из поверхностей по одной заданной проекции (в нашем случае имеющейся фронтальной проекции) линии перехода.

10.3. Пример выполнения графической работы «Пересечение поверхностей»

В графической работе даны две проекции пересекающихся поверхностей.

Требуется: построить третью проекцию, показать все проекции линии пересечения поверхностей и их видимость.

Числовые данные варианта взять из приложения 11.4. Номер варианта выдается преподавателем.

Оформление данной графической работы выполняется аналогично вышеприведенным графическим работам (прил. 11.1).

Начинают работу с вычерчивания на листе формата А3 по заданным размерам двух проекций пересекающихся поверхностей, в нашем случае конуса и призмы (рис. 10.5).

Построение третьей проекции и всех проекций (горизонтальной, фронтальной и профильной) линии пересечения поверхностей с их видимостью на чертеже начинают с проработки соответствующей темы данного учебного пособия и лекционного материала. Теория построение проекций линии пересечения поверхностей подробно рассмотрена в подразделе 10.2.3. данного учебного пособия. Построение на комплексном чертеже трех проекций линии пересечения прямого кругового конуса и трехгранной призмы представлено на рис. 10.5.

Рис. 10.5.Пример выполнения графической работы «Пересечение поверхностей»

Дата добавления: 2014-01-05