Примеры линеаризации нелинейных моделей

Рассмотрим пример из параграфа 1.1, предположив, что связь между признаками носит нелинейный характер, и найдем параметры следующих нелинейных уравнени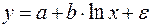й: , и .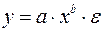

Для нахождения параметров регрессии делаем замену и составляем вспомогательную таблицу ().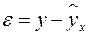

Таблица 1.5

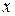
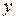
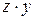
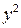
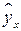
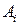
	1,2	0,182	0,9	0,164	0,033	0,81	0,499	0,401	0,1610	44,58
	3,1	1,131	1,2	1,358	1,280	1,44	1,508	-0,308	0,0947	25,64
	5,3	1,668	1,8	3,002	2,781	3,24	2,078	-0,278	0,0772	15,43
	7,4	2,001	2,2	4,403	4,006	4,84	2,433	-0,233	0,0541	10,57
	9,6	2,262	2,6	5,881	5,116	6,76	2,709	-0,109	0,0119	4,20
	11,8	2,468	2,9	7,157	6,092	8,41	2,929	-0,029	0,0008	0,99
	14,5	2,674	3,3	8,825	7,151	10,89	3,148	0,152	0,0232	4,62
	18,7	2,929	3,8	11,128	8,576	14,44	3,418	0,382	0,1459	10,05
Итого	71,6	15,315	18,7	41,918	35,035	50,83	18,720	-0,020	0,5688	116,08
Среднее значение	8,95	1,914	2,34	5,240	4,379	6,35	–	–	0,0711	14,51
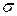
	–	0,846	0,935	–	–	–	–	–	–	–
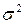
	–	0,716	0,874	–	–	–	–	–	–	–

Найдем уравнение регрессии:

,

.

Т.е. получаем следующее уравнение регрессии: 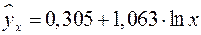. Теперь заполняем столбцы 8-11 нашей таблицы.

Индекс корреляции находим по формуле (1.21):

,

а индекс детерминации , который показывает, что 91,8% вариации результативного признака объясняется вариацией признака-фактора, а 8,2% приходится на долю прочих факторов.

Средняя ошибка аппроксимации: , что недопустимо велико.

-критерий Фишера:

,

значительно превышает табличное .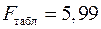

Изобразим на графике исходные данные и линию регрессии:

Рис. 1.6.

Для нахождения параметров регрессии делаем замену и составляем вспомогательную таблицу ().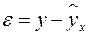

Таблица 1.6

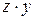
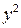
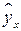
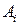
	1,2	1,10	0,9	0,99	1,2	0,81	0,734	0,166	0,0276	18,46
	3,1	1,76	1,2	2,11	3,1	1,44	1,353	-0,153	0,0235	12,77
	5,3	2,30	1,8	4,14	5,3	3,24	1,857	-0,057	0,0033	3,19
	7,4	2,72	2,2	5,98	7,4	4,84	2,247	-0,047	0,0022	2,12
	9,6	3,10	2,6	8,06	9,6	6,76	2,599	0,001	0,0000	0,05
	11,8	3,44	2,9	9,96	11,8	8,41	2,912	-0,012	0,0001	0,42
	14,5	3,81	3,3	12,57	14,5	10,89	3,259	0,041	0,0017	1,20
	18,7	4,32	3,8	16,43	18,7	14,44	3,740	0,060	0,0036	1,58
Итого	71,6	22,54	18,7	60,24	71,6	50,83	18,700	-0,001	0,0619	39,82
Среднее значение	8,95	2,82	2,34	7,53	8,95	6,35	–	–	0,0077	4,98
	–	1,00	0,935	–	–	–	–	–	–	–
	–	1,00	0,874	–	–	–	–	–	–	–

Найдем уравнение регрессии:

,

.

Т.е. получаем следующее уравнение регрессии: 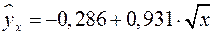. Теперь заполняем столбцы 8-11 нашей таблицы.

Индекс корреляции находим по формуле (1.21):

,

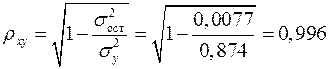а индекс детерминации 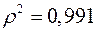, который показывает, что 99,1% вариации результативного признака объясняется вариацией признака-фактора, а 0,9% приходится на долю прочих факторов.

Средняя ошибка аппроксимации: 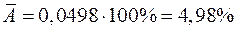показывает, что линия регрессии хорошо приближает исходные данные.

-критерий Фишера:

,

значительно превышает табличное .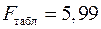

Изобразим на графике исходные данные и линию регрессии:

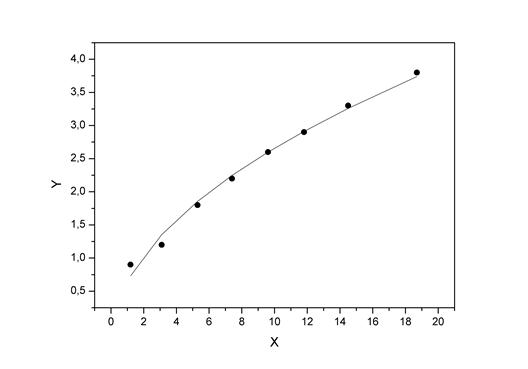
Рис. 1.7

Для нахождения параметров регрессии 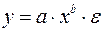необходимо провести ее линеаризацию, как было показано выше:

,

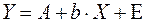где .

Составляем вспомогательную таблицу для преобразованных данных:

Таблица 1.7

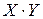
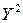
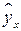
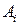
	0,182	-0,105	-0,019	0,033	0,011	0,8149	0,0851	0,0072	9,46
	1,131	0,182	0,206	1,280	0,033	1,3747	-0,1747	0,0305	14,56
	1,668	0,588	0,980	2,781	0,345	1,8473	-0,0473	0,0022	2,63
	2,001	0,788	1,578	4,006	0,622	2,2203	-0,0203	0,0004	0,92
	2,262	0,956	2,161	5,116	0,913	2,5627	0,0373	0,0014	1,43
	2,468	1,065	2,628	6,092	1,134	2,8713	0,0287	0,0008	0,99
	2,674	1,194	3,193	7,151	1,425	3,2165	0,0835	0,0070	2,53
	2,929	1,335	3,910	8,576	1,782	3,7004	0,0996	0,0099	2,62
Итого	15,315	6,002	14,637	35,035	6,266	18,608	0,0919	0,0595	35,14
Среднее значение	1,914	0,750	1,830	4,379	0,783	–	–	0,0074	4,39
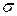
	0,846	0,470	–	–	–	–	–	–	–
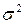
	0,716	0,221	–	–	–	–	–	–	–

Найдем уравнение регрессии:

,

.

Т.е. получаем следующее уравнение регрессии: 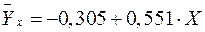. После потенцирования находим искомое уравнение регрессии:

.

Теперь заполняем столбцы 7-10 нашей таблицы.

Индекс корреляции находим по формуле (1.21):

,

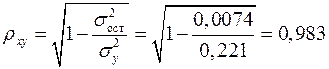а индекс детерминации 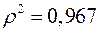, который показывает, что 96,7% вариации результативного признака объясняется вариацией признака-фактора, а 3,3% приходится на долю прочих факторов.

Средняя ошибка аппроксимации: показывает, что линия регрессии хорошо приближает исходные данные.

-критерий Фишера:

,

значительно превышает табличное .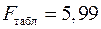

Изобразим на графике исходные данные и линию регрессии:

Рис. 1.8.

Сравним построенные модели по индексу детерминации и средней ошибке аппроксимации:

Таблица 1.8

Модель	Индекс детерминации, (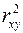, )	Средняя ошибка аппроксимации, , %
Линейная модель,	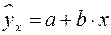0,987	6,52
Полулогарифмическая модель,	0,918	14,51
Модель с квадратным корнем,	0,991	4,98
Степенная модель,	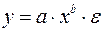0,967	4,39

Наиболее хорошо исходные данные аппроксимирует модель с квадратным корнем. Но в данном случае, так как индексы детерминации линейной модели и модели с квадратным корнем отличаются всего на 0,004, то вполне можно обойтись более простой линейной функцией.

Тестовые задания для самоконтроля

1. Какое уравнение регрессии нельзя свести к линейному виду:

а) ;

б) :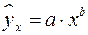

в) .

2. Какое из уравнений является степенным:

а) ;

б) :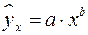

в) .

3. Параметр 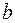в степенной модели является:

а) коэффициентом детерминации;

б) коэффициентом эластичности;

в) коэффициентом корреляции.

4. Коэффициент корреляции 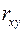может принимать значения:

а) от –1 до 1;

б) от 0 до 1;

в) любые.

5. Для функции 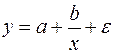средний коэффициент эластичности имеет вид:

а) ;

б) ;

в) .

6. Какое из следующих уравнений нелинейно по оцениваемым параметрам:

а) ;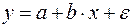

б) ;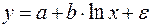

в) .

Список литературы

Основная:

1. Эконометрика [Текст]: учебник/ И. И. Елисеева, С. В. Курышев, Ю.В. Нерадовская - 3-е изд., перераб. и доп.- М.: Проспект, 2011.- 576 c.

2. Бигильдеева, Т. Б. Эконометрика [Текст]: учебное пособие/ Т. Б. Бигильдеева, Е. А. Постников.- Челябинск: Челяб. гос. ун-т, 2007.- 109 c.

1. Практикум по эконометрике: Учебное. пособие / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2008. – 192 с.

Дополнительная:

1. Айвазян, С. А. Эконометрика: Учебное пособие.- 98 с.- Гриф УМО М.: Маркет, 2007.-

2. Катышев, П. К. Сборник задач к начальному курсу эконометрики [Текст]: учебное пособие/ П. К. Катышев.- М.: Дело, 2007.- 368 c.

1. Сборник задач по эконометрике: Учебное пособие для студентов экономических вузов/ Сост. Е.Ю. Дорохина, Л.Ф. Преснякова, Н.П. Тихомиров. – М.: Издательство «Экзамен», 2003. – 224 с.
2. Эконометрика: Учебник / Тихомиров Н.П., Дорохина Е.Ю. – М.: Издательство «Экзамен», 2003. – 512 с.

Тема «Множественная регрессия и корреляция»

Цель: Разобрать понятие множественной регрессии, рассмотреть применение МНК критериев оценки существенности и качества коэффициентов регрессии в построенной модели. Выявить алгоритм отбора переменных в модель множественной регрессии.

Ключевые слова: мультиколлинеарность, стандартизированная форма уравнения, парные и межфакторные коэффициенты корреляции, МНК, эластичность.

Вопросы:

1. Спецификация модели. Отбор факторов при построении уравнения множественной регрессии

2. Метод наименьших квадратов (МНК). Свойства оценок на основе МНК.

3. Пример.

4. Проверка существенности факторов и показатели качества регрессии

5. Пример.

Дата добавления: 2014-01-05