Основные определения теории биматричных игр

Лекция № 4. Биматричные игры.

Цель: изучить особенности решения биматричных игр.

Ключевые слова: биматричная игра, решение биматричной игры, чистая и смешанная стратегия в биматричной игре.

Вопросы:

1. Основные определения теории биматричных игр

2. Смешанные стратегии в биматричных играх

3. Ситуация равновесия в биматричных играх.

Рассмотрим конфликтную ситуацию, в которой каждый из двух участников имеет следующие возможности для выбора своей линии поведения:

игрок А – может выбрать любую из стратегий А₁,..., А_т,

игрок В – любую из стратегий В₁, …, В_n

При этом всякий раз их совместный выбор оценивается вполне определенно:

если игрок А выбрал i -ю стратегию , а игрок В – k-ю стратегию , то в итоге выигрыш игрока А будет равен некоторому числу , а выигрыш игрока В некоторому, вообще говоря, другому числу .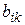

Иными словами, всякий раз каждый из игроков получает свой приз.

Последовательно перебирая все стратегии игрока А и все стратегии игрока В, мы сможем заполнить их выигрышами две таблицы (первая из них описывает выигрыши игрока А, а вторая – выигрыши игрока В).

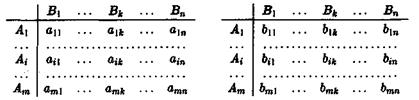
Обычно эти таблицы записывают в виде матриц

Здесь А – платежная матрица игрока А, а В – платежная матрица игрока В.

При выборе игроком А i -й стратегии, а игроком В – k -й стратегии их выигрыши находятся в матрицах выплат на пересечении i -х строк и k -x столбцов: в матрице А это элемент , а в матрице В – элемент .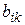

Таким образом, в случае, когда интересы игроков различны (но не обязательно противоположны), получаются две платежные матрицы: одна – матрица выплат игроку А, другая – матрица выплат игроку В. Поэтому совершенно естественно звучит название, которое обычно присваивается подобной игре – биматричная.

Замечание. Рассматриваемые матричные игры, можно рассматривать и как биматричные, где матрица выплат игроку В противоположна матрице выплат А:

В общем случае биматричная игра – это игра с ненулевой суммой.

Класс биматр. игр значительно шире класса матричных (разнообразие новых моделируемых конфликтных ситуаций весьма заметно), а, значит, неизбежно увеличиваются и трудности, встающие на пути их успешного разрешения.

Пример. «Студент — Преподаватель».

Рассмотрим следующую ситуацию. Студент (игрок А) готовится к зачету, который принимает Преподаватель (игрок В). Можно считать, что у Студента две стратегии – подготовиться к сдаче зачета (+) и не подготовиться (-). У Преподавателя также две стратегии – поставить зачет [+] и не поставить зачета [-].

В основу значений функций выигрыша игроков положим следующие соображения:

Количественно это можно выразить, например, так

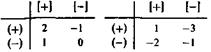
Дата добавления: 2014-01-05