Аксиомы Шепли

1. Аксиома эффективности. Если S  любой носитель игры с характеристической функцией u, то

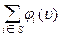= u(S)

Иными словами, справедливость требует, что при разделении общего выигрыша носителя игры ничего не выделять на долю посторонних, не принадлежащих этому носителю, равно как и ничего не взимать с них.

2. Аксиома симметрии. Для любой перестановки p и iÎN должно выполняться

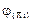(pu) = ji (u),

т.е. игроки, одинаково входящие в игру, должны по справедливости получать одинаковые выигрыши.

3. Аксиома агрегации. Если есть две игры с характеристическими функциями u¢ и u¢¢, то

j i (u¢ + u¢¢) = j i (u¢) + j i (u¢¢),

т.е. ради справедливости необходимо считать, что при участии игроков в двух играх их выигрыши в отдельных играх должны складываться.

Определение. Вектором цен (вектором Шепли) игры с характеристической функцией u называется n-мерный вектор

j (u) = (j1(u), j2(u),..., jn(u)),

удовлетворяющий аксиомам Шепли.

Существование вектора Шепли вытекает из следующей теоремы

Теорема. Существует единственная функция j, определённая для всех игр и удовлетворяющая аксиомам Шепли.

Определение. Характеристическая функция wS(T), определённая для любой коалиции S, называется простейшей, если

wS(T) =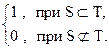

Содержательно простейшая характеристическая функция описывает такое положение дел, при котором множество игроков S выигрывает единицу тогда и только тогда, когда оно содержит некоторую основную минимальную выигрывающую коалицию S.

Можно доказать, что компоненты вектора Шепли в явном виде запишутся следующим образом

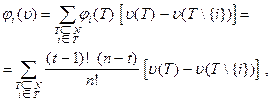
где t  число элементов в T.

Вектор Шепли содержательно можно интерпретировать следующим образом: предельная величина, которую вносит i-й игрок в коалицию T, выражается как

u(T) - u(T \{i})

и считается выигрышем i-го игрока; gi (T)  это вероятность того, что i-й игрок вступит в коалицию T \{i}; ji (u)  средний выигрыш i-го игрока в такой схеме интерпретации. В том случае, когда u  простейшая,

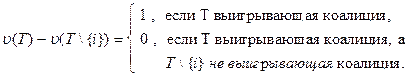
Следовательно

,

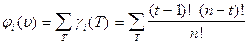где суммирование по T распространяется на все такие выигрывающие коалиции T, что коалиция T \{i}не является выигрывающей.

Пример. Рассматривается корпорация из четырёх акционеров, имеющих акции соответственно в следующих размерах

a1 = 10, a2 = 20, a3 = 30, a4 = 40.

Любое решение утверждается акционерами, имеющими в сумме большинство акций. Это решение считается выигрышем, равным 1. Поэтому данная ситуация может рассматриваться как простая игра четырёх игроков, в которой выигрывающими коалициями являются следующие:

{2; 4}, {3; 4},

{1; 2; 3}, {1; 2; 4}, {2; 3; 4}, {1; 3; 4},

{1; 2; 3; 4}.

Найдём вектор Шепли для этой игры.

При нахождении j1 необходимо учитывать, что имеется только одна коалиция T = {1; 2; 3}, которая выигрывает, а коалиция T \{1} = {2; 3} не выигрывает. В коалиции T имеется t = 3 игрока, поэтому

.

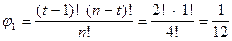Далее, определяем все выигрывающие коалиции, но не выигрывающие без 2-го игрока: {2; 4}, {1; 2; 3}, {2; 3; 4}. Поэтому

.

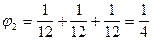Аналогично получаем, что , .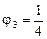

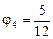В результате получаем, что вектор Шепли равен 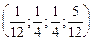. При этом, если считать, что вес голоса акционера пропорционален количеству имеющихся у него акций, то получим следующий вектор голосования

,

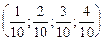который, очевидно, отличается от вектора Шепли.

Анализ игры показывает, что компоненты 2-го и 3-го игроков равны, хотя третий игрок имеет больше акций. Это получается вследствие того, что возможности образования коалиций у 2-го и 3-го игрока одинаковые. Для 1-го и 4-го игрока ситуация естественная, отвечающая силе их капитала.

Вопросы для самоконтроля:

1. Дайте определение кооперативной игры?

2. Какие виды кооперативных игр вы знаете?

3. В чем заключается основная идея решения таких игр?

Список литературы

Основная:

1. Оуэн Г. Теория игр. Учебное пособие. Санкт-Петербург: ЛКИ, 2008 – 229 с.
2. Мазалов В.В. Математическая теория игр и приложения: Учебное пособие. М.: Лань, 2010
3. Губко М.В., Новиков Д.А Теория игр в управлении организационными процессами [Электронный ресурс]: Учебное пособие. М.: Наука, 2005 – 138 с.
4. Даниловцева Е.Р., Теория игр: основные понятия: текст лекций [Электронный ресурс]. Санкт-Петербург: СПбГУАП, 2003 – 36 с.
5. Коковин С.Г., Лекции по теории игр [Электронный ресурс]. Новосибирск: Типография НГУ, 2010 г. – 91 с.

Дополнительная:

1. Самаров К.Л. Элементы теории игр [Электронный ресурс]. Учебное пособие. Новосибирск: Типография НГУ, 2010 г. – 91 с.
2. Волков Ю.И., Волков А.Ю. Теория игр [Электронный ресурс]. Тюмень, ТГИМЭУП, 2002.
3. Захаров С.Д. Курс теории игр [Электронный ресурс]. Тюмень, ТГИМЭУП, 2002.
4. Данилов В.И. Лекции по теории игр [Электронный ресурс]. КЛ/2002/001. М.: РЭШ, 2002.-192 с.

Дата добавления: 2014-01-05