
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Модуль 1 Решение задач линейного программирования
|
|
|
|
Proof.
Курс
Курс
Курс
Курс
Курс
Вычислительная схема симплексного метода
Решение задач линейного программирования
Рассмотрим симплексный метод на примере следующей задачи:
 ;
;
 ,
,
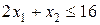 ; (3.6)
; (3.6)
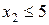 ;
;
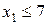 ;
;
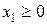 ,
, 
Решение. С помощью дополнительных неотрицательных переменных перейдем к системе уравнений вместо системы неравенств. Учитывая, что все неравенства имеют знак “ ”. Дополнительные переменные входят со знаком плюс. Исходная система ограничений после указанных преобразований имеет следующий вид:
”. Дополнительные переменные входят со знаком плюс. Исходная система ограничений после указанных преобразований имеет следующий вид:
 ,
,
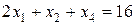 ; (3.7)
; (3.7)
 ;
;
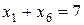 ;
;
Для нахождения первоначального базисного решения разобьем переменные на две группы: основные (базисные) и не основные (небазисные). Легко видеть, что определитель  при дополнительных переменных
при дополнительных переменных  имеет следующий вид:
имеет следующий вид:  и, следовательно, отличен от нуля. Исходя из этого переменные
и, следовательно, отличен от нуля. Исходя из этого переменные  можно взять в качестве основных переменных на первом шаге решения задачи. При выборе основных переменных на первом шаге не обязательно составлять определитель и проверять равно ли нулю его значение. Можно воспользоваться следующим правилом.
можно взять в качестве основных переменных на первом шаге решения задачи. При выборе основных переменных на первом шаге не обязательно составлять определитель и проверять равно ли нулю его значение. Можно воспользоваться следующим правилом.
В качестве основных переменных на первом шаге следует выбрать (если это возможно) такие 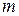 переменных, каждая из которых входит только в одно из
переменных, каждая из которых входит только в одно из 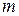 уравнений системы ограничений. В рассматриваемой ситуации дополнительные переменные удовлетворяют этому правилу.
уравнений системы ограничений. В рассматриваемой ситуации дополнительные переменные удовлетворяют этому правилу.
Шаг 1. Основные переменные  . Неосновные переменные
. Неосновные переменные 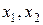 . Выразим основные переменные через неосновные переменные:
. Выразим основные переменные через неосновные переменные:
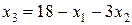 ;
;
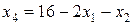 ; (3.8)
; (3.8)
 ;
;
 .
.
Положим неосновные переменные равными нулю, т.е.  , получим базисное решение
, получим базисное решение  , которое является допустимым. Учитывая, что целевая функция, выраженная через неосновные переменные, имеет вид
, которое является допустимым. Учитывая, что целевая функция, выраженная через неосновные переменные, имеет вид
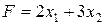 ,
,
легко понять, что ее значения при  равны нулю и может быть увеличено за счет увеличения любой их неосновных переменных
равны нулю и может быть увеличено за счет увеличения любой их неосновных переменных 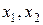 . Это можно сделать, если перейти к такому новому допустимому базисному решению, в котором эта переменная будет основной, т.е. будет принимать не нулевое, а положительное значение. При таком переходе одна из основных переменных перейдет в неосновные, а геометрически произойдет переход к соседней вершине многогранника, где значение целевой функции лучше.
. Это можно сделать, если перейти к такому новому допустимому базисному решению, в котором эта переменная будет основной, т.е. будет принимать не нулевое, а положительное значение. При таком переходе одна из основных переменных перейдет в неосновные, а геометрически произойдет переход к соседней вершине многогранника, где значение целевой функции лучше.
В данном примере, учитывая, что в целевой функции коэффициенты при 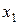 и
и  положительны, в основные переменные можно переводить и
положительны, в основные переменные можно переводить и 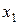 и
и  . Для определенности в основные переменные переведем ту переменную, коэффициент которой в целевой функции больше. В данном случае такой переменной является
. Для определенности в основные переменные переведем ту переменную, коэффициент которой в целевой функции больше. В данном случае такой переменной является  .
.
Поскольку необходимо сохранять допустимость решений, т.е. все переменные должны оставаться неотрицательными и, следовательно, необходимо выполнение следующих неравенств (при этом 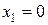 как неосновная переменная)
как неосновная переменная)
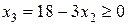
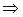
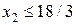 ;
;
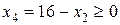
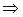
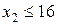 ;
;

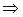
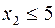 ;
;
 .
.
Каждое уравнение системы (3.8), кроме последнего, определяет оценочное отношение – границу роста переменной  , сохраняющую неотрицательность соответствующей переменной.
, сохраняющую неотрицательность соответствующей переменной.
Уравнение  не ограничивает рост переменной
не ограничивает рост переменной  , т.к. данная переменная в него не входит. В этом случае условимся обозначать границу символом
, т.к. данная переменная в него не входит. В этом случае условимся обозначать границу символом 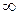 . Такой же знак будем использовать, когда свободный член и коэффициент при переменной в уравнении имеют одинаковые знаки, так как в этом случае нет ограничений на рост переменной. На рост переменной не накладывается ограничений и в том случае, когда правая часть соответствующего неравенства равна нулю, а переводимая переменная имеет положительный коэффициент. В этом случае граница обозначается символом
. Такой же знак будем использовать, когда свободный член и коэффициент при переменной в уравнении имеют одинаковые знаки, так как в этом случае нет ограничений на рост переменной. На рост переменной не накладывается ограничений и в том случае, когда правая часть соответствующего неравенства равна нулю, а переводимая переменная имеет положительный коэффициент. В этом случае граница обозначается символом 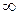 .
.
Очевидно, что сохранение неотрицательности возможно, если не нарушена ни одна из границ. Следовательно, в рассматриваемом случае
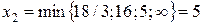 .
.
При  переменная
переменная  обращается в нуль и переходит в неосновные переменные. Уравнение, где достигается наибольшее возможное значение переменной, переводимой в основные (т.е. где оценка минимальна), называется разрешающим. В данном случае - это третье уравнение.
обращается в нуль и переходит в неосновные переменные. Уравнение, где достигается наибольшее возможное значение переменной, переводимой в основные (т.е. где оценка минимальна), называется разрешающим. В данном случае - это третье уравнение.
Шаг 2. Основные переменные  . Неосновные переменные
. Неосновные переменные  .
.
На этом шаге из уравнения (3.8) выразим новые основные переменные, начиная с разрешающего уравнения (оно используется при выражении записи для  )
)
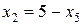 ;
;
 ;
;
 ;
;
 .
.
Преобразуя систему, получим:
 ;
;
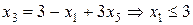 ; (3.9)
; (3.9)
 ;
;
 .
.
Второе базисное решение  является допустимым.
является допустимым.
Выразим значение целевой функции, получим:
 .
.
Изменение значения целевой функции можно определить заранее как произведение наибольшего возможного значения переменной, переводимой в основные, на ее коэффициент в выражении для целевой функции. В рассматриваемом примере
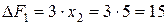 ;
;  .
.
Далее, как легко видеть, значение 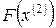 не является максимальным, поскольку оно может быть улучшено за счет переменной
не является максимальным, поскольку оно может быть улучшено за счет переменной 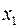 , входящей в выражение для целевой функции с положительным коэффициентом. Как и ранее предположив, что правые части уравнений (3.9) неотрицательны, получим, что наибольшее значение
, входящей в выражение для целевой функции с положительным коэффициентом. Как и ранее предположив, что правые части уравнений (3.9) неотрицательны, получим, что наибольшее значение 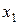 определяется из выражения
определяется из выражения
 .
.
Второе уравнение является разрешающим, переменная  переходит в неосновные при этом
переходит в неосновные при этом  .
.
Шаг 3. Основные переменные  . Неосновные переменные
. Неосновные переменные  .
.
Повторяя процедуру шага 2, выражаем новые основные переменные через неосновные, начиная с разрешающего уравнения. Проведя необходимые преобразования, получим
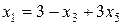 ;
;
 ; (3.10)
; (3.10)
 ;
;
 .
.
Базисное решение  соответствует вершине, у которой
соответствует вершине, у которой  ;
;  . Выражаем линейную функцию через неосновные переменные:
. Выражаем линейную функцию через неосновные переменные:
 ;
;
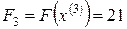 .
.
Проверяем  .
.
Третье допустимое базисное решение не является оптимальным, так как при неосновной переменной 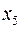 в выражении для целевой функции через неосновные переменные содержится положительный коэффициент. Переводим
в выражении для целевой функции через неосновные переменные содержится положительный коэффициент. Переводим 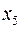 в основную переменную. При определении наибольшего возможного значения для
в основную переменную. При определении наибольшего возможного значения для 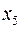 получаем, рассмотрев все четыре уравнения системы (3.10)
получаем, рассмотрев все четыре уравнения системы (3.10)
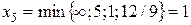 .
.
Третье уравнение является разрешающим и переменная  переходит в неосновные
переходит в неосновные  .
.
Шаг 4. Основные переменные 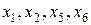 . Неосновные переменные
. Неосновные переменные  .
.
После преобразований получим
 ;
;
 ;
;
 ; (3.11)
; (3.11)
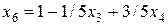 .
.
Базисное решение 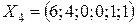 .
.
Целевая функция, выраженная через основные переменные, имеет вид
 .
.
Это выражение не содержит положительных коэффициентов при неосновных переменных, следовательно, улучшить решение нельзя и поэтому значение целевой функции  максимальное.
максимальное.
На основе изучения рассмотренного примера критерий оптимальности решения при отыскании максимума целевой функции может быть сформулировано так: если в выражении целевой функции через неосновные переменные отсутствуют положительные коэффициенты при неосновных переменных, то решение оптимальною.
При решении задачи определения минимума целевой функции можно использовать один из следующих путей:
- если необходимо отыскать минимум  , то решается задача максимизации функции
, то решается задача максимизации функции  , и это решение принимается за решение исходной задачи;
, и это решение принимается за решение исходной задачи;
- на каждом шаге симплексного метода уменьшать целевую функцию за счет той неосновной переменной, которая входит в выражение целевой функции с отрицательным коэффициентом.
Рассмотрим симплексный метод решения следующей задачи на минимум.
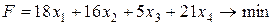 .
.
 ; (3.12)
; (3.12)
 ;
;
 ,
, 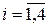 .
.
Сведем данную задачу к каноническому виду, для чего введем положительные дополнительные переменные с отрицательным знаком, т.к. неравенства имеют вид  .
.
Получим систему уравнений
 ;
;
 .
.
Шаг 1. Выберем в качестве основных переменных переменные  . Неосновные переменные
. Неосновные переменные  .
.
Выразим основные переменные через неосновные переменные:
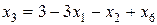 ;
;
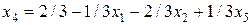 .
.
Первое базисное решение получим, приравняв нулю все неосновные переменные:  . Учитывая, что все координаты неотрицательны, это решение допустимо Выразим линейную целевую функцию
. Учитывая, что все координаты неотрицательны, это решение допустимо Выразим линейную целевую функцию  через неосновные переменные:
через неосновные переменные:

Значение  не является оптимальным, так как функцию
не является оптимальным, так как функцию  можно уменьшить за счет перевода в основные переменные любую из переменных
можно уменьшить за счет перевода в основные переменные любую из переменных  , имеющих в выражении для
, имеющих в выражении для  отрицательные коэффициенты. Так как
отрицательные коэффициенты. Так как 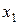 имеет больший по абсолютному значению коэффициент, то переводим в основные именно эту переменную.
имеет больший по абсолютному значению коэффициент, то переводим в основные именно эту переменную.
Для нее наибольшее возможное значение определяется из соотношения 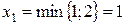 . То есть первое уравнение становится разрешающим.
. То есть первое уравнение становится разрешающим.
Следовательно,  становится неосновной переменной,
становится неосновной переменной, 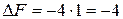 .
.
Шаг 2. Основные переменные 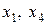 . Неосновные переменные
. Неосновные переменные 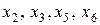 .
.
| Дата | Время | Предмет | Преподаватель | Аудитор. |
| 13 окт (суб.) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Общее собрание курса Отечественная история Ин. яз. Информатика | Папуша Е.А. Гришина (англ) Шелудько (нем) к.т.н. Кильдишов В.Д. | № 16 № 16 № 15 № 9 № 19 |
| 14 окт. (воскр) | 9.40. – 12.30. 13.00.-15.50. | Математика УП: Введение в УП МО: Введение в туризм | к.т.н. Пунин И.П. к.п.н. Панкратова Е.Н. Мелюх Е.А. | № 16 № 16 № 7 |
| 20 окт (суб.) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Информатика Ин. яз. УП: Мотивац. труда МО: Рекреационное ресурсоведение | к.т.н. Кильдишов В.Д. Гришина (англ) Шелудько (нем) к.п.н. Панкратова Е.Н. Вознюк В.Н. | № 19 № 15 № 9 № 16 № 5 |
| 21 окт (воскр) | 9.40. – 12.30. 13.00.-15.50. | Отечественная история Математика | Папуша Е.А. к.т.н. Пунин И.П. | № 16 № 16 |
| 27 окт (суб.) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | УП: Мотивац. труда МО: Рекреационное ресурсоведение Ин. яз. ОБЖ | к.п.н. Панкратова Е.Н. Вознюк В.Н. Гришина (англ) Шелудько (нем) к.в.н. Прокопенков И.П. | № 16 № 5 № 15 № 9 № 6 |
| 28 окт (воскр) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Математика УП: Введение в УП МО: Введение в туризм УП: Мотивац. труда | к.т.н. Пунин И.П. к.п.н. Панкратова Е.Н. Мелюх Е.А. к.п.н. Панкратова Е.Н. | № 16 № 16 № 7 № 16 |
| 03 ноябр (суб.) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | УП: Мотивац. труда МО: Рекреационное ресурсоведение Ин. яз. ОБЖ | к.п.н. Панкратова Е.Н. Вознюк В.Н. Гришина (англ) Шелудько (нем) к.в.н. Прокопенков И.П. | № 16 № 5 № 15 № 9 № 6 |
| 04 ноябр (воскр) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Отечественная история Математика УП: Введение в УП МО: Введение в туризм | Папуша Е.А. к.т.н. Пунин И.П. к.п.н. Панкратова Е.Н. Мелюх Е.А. | № 16 № 16 № 16 № 7 |
Расписание лекционной сессии заочной формы обучения
| Дата | Время | Предмет | Преподаватель | Аудитор. |
| 13 окт (суб.) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Ин. яз. Информатика Основы менеджмента | Гришина(англ) Шелудько (нем) к.т.н. Кильдишов В.Д. к.т.н. Борисов К.В. | № 15 № 9 № 19 № 24 |
| 14 окт. (воскр) | 9.40. – 12.30. 13.00.-15.50. | Русский язык/культура речи Экономическая теория | Федотова М.М. Бурлуцкий Р.В. | № 17 № 17 |
| 20 окт (суб.) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Ин. яз. Информатика Планирование карьеры | Гришина(англ) Шелудько (нем) к.т.н. Кильдишов В.Д. к.т.н. Борисов К.В. | № 15 № 9 № 19 № 17 |
| 21 окт (воскр) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Основы менеджмента Экономическая теория Русский язык/культура речи | к.т.н. Борисов К.В. Бурлуцкий Р.В. Федотова М.М. | № 24 № 17 № 17 |
| 27 окт (суб.) | 9.40. – 12.30. 13.00.-15.50. | Ин. яз. Русский язык/культура речи | Гришина(англ) Шелудько (нем) Федотова М.М. | № 15 № 9 № 17 |
| 28 окт (воскр) | 9.40. – 12.30. 13.00.-15.50. | Планирование карьеры Экономическая теория | к.т.н. Борисов К.В. Бурлуцкий Р.В. | № 17 № 17 |
| 03 ноябр (суб.) | 9.40. – 12.30. 13.00.-15.50. | Ин. яз. Основы менеджмента | Гришина (англ) Шелудько (нем) к.т.н. Борисов К.В. | № 15 № 9 № 24 |
| 04 ноябр (воскр) | 9.40. – 12.30. 13.00.-15.50. | Основы менеджмента Планирование карьеры | к.т.н. Борисов К.В. к.т.н. Борисов К.В. | № 24 № 17 |
Расписание лекционной сессии заочной формы обучения
3 курс – СПЕЦИАЛИСТЫ
| Дата | Время | Предмет | Преподаватель | Аудитор. |
| 13 окт (суб.) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Информатика Статистика Основы менеджмента | к.т.н. Кильдишов В.Д. к.т.н. Пунин И.П.. к.т.н. Борисов К.В. | № 19 № 20 № 24 |
| 14 окт. (воскр) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Бухучет Статистика Правоведение | Шабанова Н.Ю. к.т.н. Пунин И.П.. к.п.н. Царев А.С. | № 20 № 20 № 20 |
| 20 окт (суб.) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Правоведение УП: Планир. карьеры МО:Реклама в проф деят. Ин. яз. | к.п.н. Царев А.С. к.т.н. Борисов К.В. к.п.н. Макашин В.В. Пичененко/Гришина Шелудько | № 20 № 6 № 7 № 15, 4, |
| 21 окт (воскр) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Основы менеджмента Информатика Статистика | к.т.н. Борисов К.в. к.т.н. Кильдишов В.Д. к.т.н. Пунин И.П.. | № 24 № 19 № 20 |
| 27 окт (суб.) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Бухучет Правоведение Ин. яз. | Шабанова Н.Ю. к.п.н. Царев А.С. Пичененко/Гришина/Ше лудько | № 20 № 20 № 15, 4, |
| 28 окт (воскр) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | УП: Планир. карьеры МО:Реклама в проф деят. Статистика Бухучет | к.т.н. Борисов К.В. к.п.н. Макашин В.В. к.т.н. Пунин И.П. Шабанова Н.Ю. | № 17 № 7 № 20 № 20 |
| 03 ноябр (суб.) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Бухучет Основы менеджмента Ин. яз. | Шабанова Н.Ю. к.т.н. Борисов К.В. Пичененко/Гришина/ Шелудько | № 20 № 24 № 15, 4, |
| 04 ноябр (воскр) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Основы менеджмента УП: Планир. карьеры МО:Реклама в проф деят. Информатика | к.т.н. Борисов К.В. к.т.н. Борисов К.В. к.п.н. Макашин В.В. к.т.н. Кильдишов В.Д. | № 24 № 17 № 7 № 19 |
Расписание лекционной сессии заочной формы обучения
3 курс – БАКАЛАВРЫ
| Дата | Время | Предмет | Преподаватель | Аудитор. |
| 13 окт (суб.) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | УП: Аудит персонала МО: Управление персоналом Статистика Основы менеджмента | к.в.н. Прокопенков И.П. д.п.н. Давыдова Г.И. к.т.н. Пунин И.П. к.т.н. Борисов К.В. | № 6 № 7 № 20 № 24 |
| 14 окт. (воскр) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Бухучет Статистика Правоведение | Шабанова Н.Ю. к.т.н. Пунин И.П.. к.п.н. Царев А.С. | № 20 № 20 № 20 |
| 20 окт (суб.) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | УП: Аудит персонала МО: Реклама в проф деятельноти Правоведение Ин. яз. | к.в.н. Прокопенков И.П. к.п.н. Макашин В.В. Царев А.С. Пичененко/Гришина/ Шелудько | № 6 № 7 № 16 № 15, 4, |
| 21 окт (воскр) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Основы менеджмента УП: Охрана труда МО: Управление персоналом Статистика | к.т.н. Борисов К.В. Комовкина Е.В. д.п.н. Давыдова Г.И. к.т.н. Пунин И.П. | № 24 № 6 № 7 № 20 |
| 27 окт (суб.) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Бухучет УП: Аудит персонала МО: Управление персоналом Ин. яз. | Шабанова Н.Ю. к.в.н. Прокопенков И.П. д.п.н. Давыдова Г.И. Пичененко/Гришина/ Шелудько | № 20 № 6 № 7 № 15, 4, |
| 28 окт (воскр) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Правоведение Статистика Бухучет | к.п.н. Царев А.С. Пунин И.П. Шабанова Н.Ю. | № 6 № 20 № 20 |
| 03 ноябр (суб.) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Бухучет Основы менеджмента Ин. яз. | Шабанова Н.Ю. к.т.н. Борисов К.В. Пичененко/Гришина/ Шелудько | № 20 № 24 № 15, 4, |
| 04 ноябр (воскр) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Основы менеджмента УП: Охрана труда МО: Реклама в проф. деятельности УП: Охрана труда МО: Реклама в проф. деятельности | к.т.н. Борисов К.В. Комовкина Е.В. к.п.н. Макашин В.В. Комовкина Е.В. к.п.н. Макашин В.В. | № 24 № 6 № 7 № 6 № 20 |
Расписание лекционной сессии заочной формы обучения
| Дата | Время | Предмет | Преподаватель | Аудитор. |
| 14 окт (воскр) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Инновац. менеджмент Инновац. менеджмент УП:Управление трудовыми ресурсами | д.э.н Возняк В.Я. д.э.н Возняк В.Я. к.п.н. Панкратова Е.Н. | № 21 № 21 № 6 |
| 20 окт (суб.) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | УП:Управление трудовыми ресурсами Ин. яз. УП: Мотивация и стимулирование труда МО: МТО | к.п.н. Панкратова Е.Н. Пичененко/Сапунова/Шелудько к.п.н. Панкратова Е.Н. к.п.н. Борисов Вит. К. | № 21 № 21, 4, 9 № 16 № 6 |
| 21 окт (воскр) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50 | Психология делового общения Маркетинг Мировая экономика | д.п.н. Давыдова Г.И. к.п.н. Макашин В.В. д.э.н. Беляев М.И. | № 21 № 21 № 21 |
| 27 окт (суб.) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | УП: Мотивация и стимулирование труда МО: МТО Ин. яз. УП: Управление трудовыми ресурсами | к.п.н. Панкратова Е.Н. к.п.н. Борисов Вит. К. Пичененко /Сапунова /Шелудько к.п.н. Панкратова Е.Н. | № 16 № 6 № 21, 4, № 21 |
| 28 окт (воскр) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Мировая экономика Инновац. менеджмент УП: Мотивация и стимулирование труда МО: МТО | д.э.н. Беляев М.И. д.э.н Возняк В.Я. к.п.н. Панкратова Е.Н. к.п.н. Борисов Вит. К. | № 21 № 21 № 16 № 6 |
| 03 ноябр (суб.) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | УП: Мотивация и стимулирование труда МО: МТО Ин. яз. УП: Управление трудовыми ресурсами | к.п.н. Панкратова Е.Н. к.п.н. Борисов Вит. К. Пичененко/Сапунова/Шелудько к.п.н. Панкратова Е.Н. | № 16 № 6 № 21. 4, 9 № 17 |
| 04 ноябр (воскр) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Маркетинг Психология делового общения Мировая экономика | к.п.н. Макашин В.В. д.п.н. Давыдова Г.И. д.э.н. Беляев М.И. | № 21 № 21 № 21 |
Расписание лекционной сессии заочной формы обучения
| Дата | Время | Предмет | Преподаватель | Аудитор. |
| 20 окт (суб.) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Гос. и муниципал управление Хозяйственное право УП: Соц технологии в кадровой службе МО: Управление персоналом | к.ю.н. Дашко О.В. к.ю.н. Дашко О.В. Бурлуцкий Р.В. д.п.н. Давыдова Г.И. | № 22 № 22 № 22 № 23 |
| 21 окт (воскр) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | УП: Соц технологии в кадровой службе МО: Управлен. качеством УП: Управлен. социальн. развитием организации МО: ДТА МО: Управление персоналом | Бурлуцкий Р.В. к.т.н. Пунин И.П. к.т.н. Борисов К.В. к.п.н. Борисов Вит. К. д.п.н. Давыдова Г.И. | № 23 № 22 № 22 № 23 № 22 |
| 27 окт (суб.) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Гос. и муниципал управление Хозяйственное право МО: Управление персоналом | к.ю.н. Дашко О.В. к.ю.н. Дашко О.В. д.п.н. Давыдова Г.И. | № 22 № 22 № 22 |
| 28 окт (воскр) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | МО: ДТА УП: Управлен. социальн. развитием организации МО: ДТА МО: Управление качеством | к.п.н. Борисов Вит. К. к.т.н. Борисов К.В. к.п.н. Борисов Вит. К. к.т.н. Пунин И.П. | № 23 № 23 № 22 № 22 |
| 03 ноябр (суб.) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Гос. и муниципал управление Хозяйственное право УП: Управлен. социальн. развитием организации | к.ю.н. Дашко О.В. к.ю.н. Дашко О.В. к.т.н. Борисов К.В. | № 22 № 22 № 22 |
Расписание лекционной сессии заочной формы обучения
| Дата | Время | Предмет | Преподаватель | Аудитор. |
| 20 окт (суб.) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Стратегич менеджмент Антикризисное управлен Эконом и соц труда | к.т.н. Борисов К.В. д.э.н. Возняк В.Я. к.ф.н. Карташова Л.Э. | № 24 № 24 № 24 |
| 21 окт (воскр) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50 | Информационные технологии управления Логистика Стратегический менеджмент | кт.н. Кильдишов В.Д. .к.п.н. Егоров Н.В. к.т.н. Борисов К.В. | № 19 № 24 № 24 |
| 27 окт (суб.) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Стратегич менеджмент Антикризисное управлен. Логистика | к.т.н. Борисов К.В. д.э.н. Возняк В.Я. .к.п.н. Егоров Н.В. | № 24 № 24 № 24 |
| 28 окт (воскр) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Антикризисное управлен. Эконом и соц труда Информационные технологии управления | д.э.н. Возняк В.Я. к.ф.н. Карташова Л.Э. кт.н. Кильдишов В.Д. | № 24 № 24 № 19 |
| 03 ноябр (суб.) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Стратегич менеджмент Антикризисное управлен Эконом и соц труда | к.т.н. Борисов К.В. д.э.н. Возняк В.Я. к.ф.н. Карташова Л.Э. | № 24 № 24 № 24 |
| 04 ноябр (воскр) | 9.40. – 12.30. 13.00.-15.50. 16.00.-18.50. | Общее собрание курса Информационные технологии управления Эконом и соц труда | Панкратова Е.Н. кт.н. Кильдишов В.Д. к.ф.н. Карташова Л.Э. | № 24 № 19 № 24 |
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 507; Нарушение авторских прав?; Мы поможем в написании вашей работы!