Теорема 4. Число сочетаний с повторениями

Лекция 3.

Число r -сочетаний с повторениями из n -множества равно

.

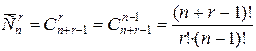# 1 способ – доказательство Эйлера.

Пусть дано n -множество S. Пронумеруем все его элементы, т.е. множеству S взаимно однозначно поставим в соответствие множество S’: S «S’ ={1, …, n } – номера элементов из S. Тогда r -выборке из S однозначно соответствует выборка r натуральных чисел из S’. Т.к. в сочетании порядок не важен, r -выборку натуральных чисел можно расположить так, чтобы

a ₁ £ a ₂ £ … £ a_r (1)

(где a_i – выбранное натуральное число). Между числами стоит знак £, т.к. выборка с повторениями и числа могут повторяться (например, а₂ и а₃ могут быть одним и тем же числом).

Добавим в выборке (1) к а₁ ноль, к а₂ – 1, к а₃ – 2 и т.д., т.е. получим выборку

a ₁+0 < a ₂+1 < … < a_r+r -1 (2)

Выборка (2) взаимно однозначно соответствует выборке (1), причём в ней нет одинаковых чисел (неравенство строгое). Следовательно, выборка (2) – это r -выборка без повторений из множества S’’` ={1, …, n, n +1, n +2, …, n+r -1}, S’’ - (n+r -1)-множество.

Таким образом, Эйлер свёл задачу о числе r -сочетаний с повторениями из n -множества к числу r -сочетаний без повторений из (n+r -1)-множества.

2 способ – доказательство Виленкина или метод словесной индукции.

Рассмотрим доказательство на примере. Пусть S ={ a, b, c, d, e }, 5-множество (n =5). Выберем некоторые сочетания с повторениями из S по три буквы (r =3), например,

abb ccc bee.

Возьмем последовательность abcde и добавим к ней каждое из этих сочетаний:

abcdeabb abcdeccc abcdebee.

Разделим элементы полученных выборок перегородками:

a|b|c|d|e|a|b|b a|b|c|d|e|c|c|c a|b|c|d|e|b|e|e.

В любой из этих выборок по 7 перегородок. Если во множестве S n элементов, а нас интересует число r -сочетаний, то в построенных аналогичным способом выборках можно поместить n + r -1 перегородок (7=5+3-1).

Поскольку в сочетаниях порядок не важен, перегруппируем буквы так, чтобы одинаковые буквы располагались рядом (изменение порядка элементов сочетание не изменяет):

aa|bbb|c|d|e a|b|cccc|d|e a|bb|c|d|eee.

Здесь разделители разделяют группы одинаковых букв. Поскольку различных букв всего 5, разделителей в любой такой выборке 4. (Если во множестве S n элементов, то в выборке можно поставить n -1 разделитель групп одинаковых элементов).

Итак, в выборках есть (n + r -1) мест для размещения перегородок, а нужно разместить (n -1) перегородку. Задача свелась к установке n -1 перегородки на n+r- 1 мест. Для каждого конкретного сочетания существует единственный способ установки перегородок, т.е. способ выбрать n -1 место из n+r -1. Поскольку перегородки не различаются, количество способов их расставить – это количество сочетаний по n -1 из n+r -1.

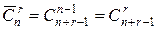
(второе равенство в силу свойства симметричности ).

3 способ – доказательство с помощью рекуррентной формулы.

Метод базируется на получении формулы, позволяющей вычислять значения искомой величины шаг за шагом, исходя из известных начальных значений и значений, вычисленных на предыдущих шагах.

Рекуррентная формула r -го порядка – формула вида

a_n = f (n, a_{n- 1}, a_{n- 2}, …, a_n-r).

Формула выражает при n>r каждый член последовательности { a_i } через предыдущие r членов. Построение рекуррентной формулы состоит из следующих шагов.

1. Выработка начальных условий исходя из каких-либо очевидных соотношений.

Обозначим 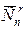через f (n,r). Очевидно, что

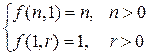(1)

2. Логические рассуждения. Зафиксируем какой-либо элемент во множестве S. Тогда относительно любого r -сочетания с повторениями из n -множества S можно сказать, содержит ли оно данный зафиксированный элемент или нет.

Если содержит, то остальные (r -1) элемент можно выбрать f (n, r -1) способами.

Если не содержит (в выборке этого элемента нет), то r -сочетание составлено из элементов (n -1)-множества (множество S за исключением данного зафиксированного элемента). Число таких сочетаний f (n -1, r).

Т.к. эти случаи взаимоисключающие, то по правилу суммы

(2)

3. Проверка формулы на некоторых значениях и вывод общей закономерности.

1) Вычислим f (n,0). Из (2) следует

. (3)

Тогда f (n,0)= f (n,1)- f (n -1,1). Из (1) f (n,1)= n, f (n -1,1)= n -1.

Следовательно, f (n,0)= n -(n -1)=1=.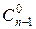

2) f (n,1) = f (n,0)+ f (n -1,1) = 1+ n- 1 = n = = .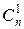

3) f (n,2) = f (n,1)+ f (n -1,2) = n + f (n -1,1)+ f (n -2,2) = n +(n -1)+ f (n -2,1)+ f (n -3,2) = … =

= n +(n -1)+…+2+1 = .

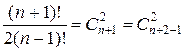(сумма арифметической прогрессии)

4) f (n,3) = f (n,2)+ f (n -1,3) = + f (n -1,2)+ f (n -2,3) = ++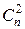 f (n -2,2)+ f (n -3,3) = … =

.

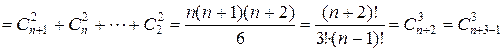(сумма геометрической прогрессии)

5) f (n,4) =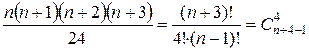

На основе частных случаев можно предположить, что

Дата добавления: 2014-01-05