Следствие 5

Следствие 3.

Следствие 2.

Следствие 1.

Так как ,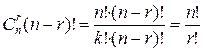

то .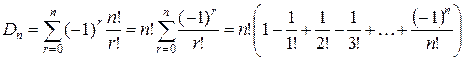

Так как 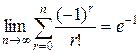, то .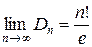

Рекуррентная формула для числа беспорядков: .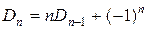

#

#

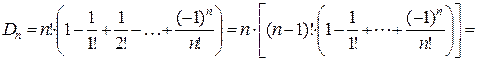
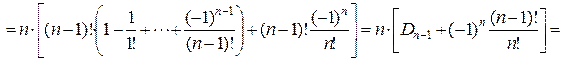
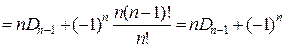Следствие 4.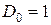

# По рекуррентной формуле из следствия 3 получаем 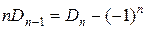или 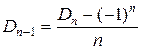. При n =1 получаем 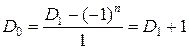. По формуле из следствия 1 получаем 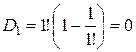. Следовательно, . #

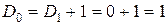Ещё одна рекуррентная формула для числа беспорядков: .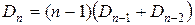

# Рассмотрим n элементов x ₁, x₂, …, x_n. Переставим их так, чтобы получить беспорядок. Начнём с x ₁: возьмём x ₁ и подставим его на место i -го элемента (i ¹1). Тогда x_i можно поставить на либо на первое место, либо на какое-то другое, кроме i- го. Если x ₁ стоит на i -м месте, а x_i – на 1-ом, то число таких беспорядков – D_{n -2} (т.е. число беспорядков оставшихся n -2 элементов). Если x ₁ не стоит на первом месте, то такой беспорядок определяется условием:

x ₂ не стоит на 2-м месте,

x ₃ не стоит на 3-м месте,

…

x_{i -1} не стоит на (i -1)-м месте,

x_i не стоит на 1-м месте,

x_{i+ 1} не стоит на (i +1)-м месте,

…

x_n не стоит на n -м месте.

Всего здесь n -1 элемент, то есть число таких беспорядков – D_{n -1}.

Итак, если x ₁ стоит на i -ом месте, то число таких беспорядков D_{n -1}+ D_n-2. Но x ₁ можно поставить на любое из (n -1) мест (кроме 1-го). Для каждой установки x ₁ справедливы приведённые выше рассуждения.

Таким образом, общее число беспорядков – (n -1)(D_{n- 1}+ D_n-2). #

Для проверки полученной формулы вычислим количество беспорядков для некоторых значений n по рекуррентной и прямой формулам. По следствию 4, D ₀=1, D ₁=0.

Рекуррентная формула	Нерекуррентная формула

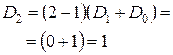
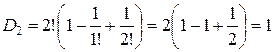
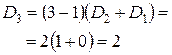
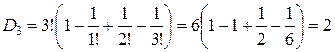
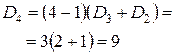
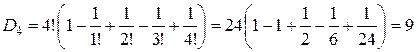
Для строгого доказательства правильности рекуррентной формулы, проверим ее в общем виде.

.

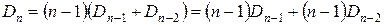Из следствия 3 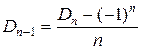, следовательно, 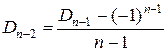. Тогда

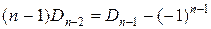. Подставим этот результат в рекуррентную формулу:

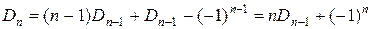. Получили формулу из следствия 3.

Обозначим через D_n,r число перестановок, в которых на своих местах остаются r элементов, а остальные (n-r) образуют беспорядок. Ясно, что D_n,n =1 (все элементы на своих местах), и D_n,0=D_n (ни одного элемента нет на своём месте).

Теорема. .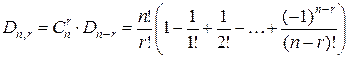

# r элементов, стоящих на своём месте, можно выбрать из n элементов 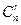способами. Для каждой такой выборки остальные (n-r) элементов образуют беспорядки, число которых D_n-r. Следовательно, всего таких перестановок .

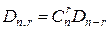С другой стороны, (n-r) элементов, образующих беспорядки, можно выбрать 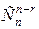способами. Следовательно, 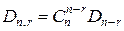. В силу симметричности биномиальных коэффициентов 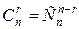, обе формулы дают один и тот же результат.

#

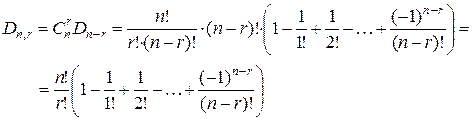Пример. Выстраиваем 5 человек в определённом порядке, после чего 3 из них переставляем так, чтобы они не стояли на своих местах. Сколько таких перестановок?

Ответ: если трое не стоят на своих местах, то оставшиеся двое стоят на своих местах, т.е.

.

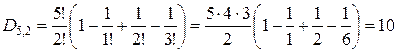Следствие. .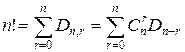

# Из n элементов можно образовать n! перестановок без повторений.

Среди них будет D_n,0 таких, где ни один элемент не стоит на своём месте;

D_{n ,1} таких, где по одному элементу стоит на своём месте;

D_{n ,2} таких, где по паре элементов стоит на своих местах;

и т.д.;

D_n,n =1 таких, где все элементы стоят на своих местах.

Следовательно, общее число перестановок (n!) равно сумме этих чисел. #

Лекция 6. Приложения метода включения и исключения в теории чисел

Дата добавления: 2014-01-05