Экспоненциальные производящие функции

1. Поскольку , то . Следовательно, если разложить бином Ньютона (1+ x) ⁿ в ряд Телора-Маклорена в окрестности точки x =0, то коэффициенты при в этом разложении есть числа r -перестановок без повторений из n -множества.

Определение. Функция вида

называется экспоненциальной производящей функцией. Экспоненциальные производящие функции позволяют находить числа различных перестановок.

Одна и та же функция может быть и полиномиальной производящей функцией, и экспоненциальной производящей функцией. Например, бином Ньютона (1+ x) ⁿ является как полиномиальной производящей функцией для чисел сочетаний без повторений (при разложении бинома в ряд по x^r), так и экспоненциальной производящей функцией для чисел перестановок без повторений (при разложении бинома в ряд по ). При n =4:

.

Проверим: ; ; ; ; .

2. Определим экспоненциальную производящую функцию для чисел перестановок с неограниченными повторениями. Известно, что число r -перестановок из n -множества с повторениями равен . Значит, ряд Тейлора-Маклорена производящей функции для этих чисел в окрестности точки x =0 должен выглядеть так: 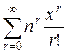. Выполним преобразования:

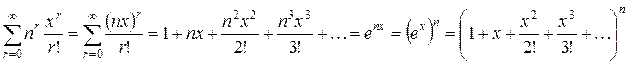Следовательно, функция является экспоненциальной производящей функцией для чисел r -перестановок с неограниченными повторениями из n -множества, а ряд соответствует предметам одного типа при построении экспоненциальных производящих функций для нахождения чисел различных перестановок.

3. Пусть перестановки образуются из конечного множества предметов: n ₁ предметов первого типа, n ₂ предметов второго типа, …, n_k предметов k -го типа (n ₁+ n ₂+…+ n_k = n). Тогда при построении экспоненциальной функции для элементов i -го типа ряд ограничивается членом 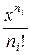. А вся экспоненциальная производящая функция для решения этой задачи выглядит так:

.

Если раскрыть скобки и привести подобные, то коэффициент при будет равен числу r ‑перестановок с ограниченными повторениями. В частности, последний член ряда будет равен

.

Коэффициент при дает нам число перестановок n предметов, из которых n ₁ предметов первого типа, n ₂ предметов второго типа, …, n_k предметов k -го типа (n ₁+ n ₂+…+ n_k = n). Эта формула совпадает с ранее полученной другим способом формулой (см., например, задачу о составлении меню из яблок, апельсинов и мандаринов).

Правила построения экспоненциальных производящих функций:

1. Каждому сорту предметов соответствует одна скобка.

2. Каждой скобке сумма .

3. Если предмет данного сорта может не входить в перестановку, то в скобке присутствует единица.

4. Ели предмет данного сорта может входить в перестановку только один раз, то в скобке присутствует х, если дважды – 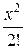, если трижды – 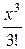, и т.д.

5. Если допускаются неограниченные повторения, то сумма в скобке бесконечна.

Правила использования экспоненциальных производящих функций:

1. Производящую функцию разложить в ряд по .

2. Пользуясь заменой переменных, привести ряд к виду 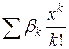(чтобы х был в степени одной буквы и делился на факториал этой же буквы). В этом случае коэффициент при 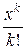даёт формулу для числа k -перестановок при заданных условиях.

3. Подставив в эту формулу (в β_k) конкретные значения k и n, получим ответ на конкретный вопрос о числе k -перестановок.

Дата добавления: 2014-01-05