Лекция 2. Структура механизмов

Классификация кинематических пар

Кинематические пары (КП) классифицируются по следующим признакам:

1) по виду места контакта (места связи) поверхностей звеньев:

- низшие, в которых контакт звеньев осуществляется по плоскости или поверхности (пары скольжения);

- высшие, в которых контакт звеньев осуществляется по линиям или точкам (пары, допускающие скольжение с перекатыванием). Они имеются, например, в зубчатых и кулачковых механизмах).

2) по относительному движению звеньев, образующих пару:

- вращательные;

- поступательные;

- цилиндрические;

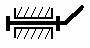
- сферические;

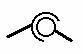
- винтовые;

- плоские.

Механизм, звенья которого образуют только вращательные, поступательные, цилиндрические и сферические пары, называют рычажным.

3) по способу замыкания (обеспечения контакта звеньев пары):

- силовое (за счет действия сил веса или силы упругости пружины);

- геометрическое (за счет конструкции рабочих поверхностей пары).

Рис.2.1 Рис.2.2

4) по числу подвижностей в относительном движении звеньев.

5) по числу условий связи, накладываемых на относительное движение звеньев (число условий связи определяет класс кинематической пары);

Тело, находясь в пространстве (в декартовой системе координат X, Y, Z) имеет 6 степеней свободы. Оно может перемещаться вдоль каждой из трёх осей X, Y и Z, а также вращаться вокруг каждой оси (рис. 2.3). Если тело (звено) образует с другим телом (звеном) кинематическую пару, то оно теряет одну или несколько из этих 6 степеней свободы.

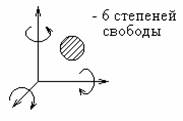
Рис. 2.3. Степени свободы тела в пространстве

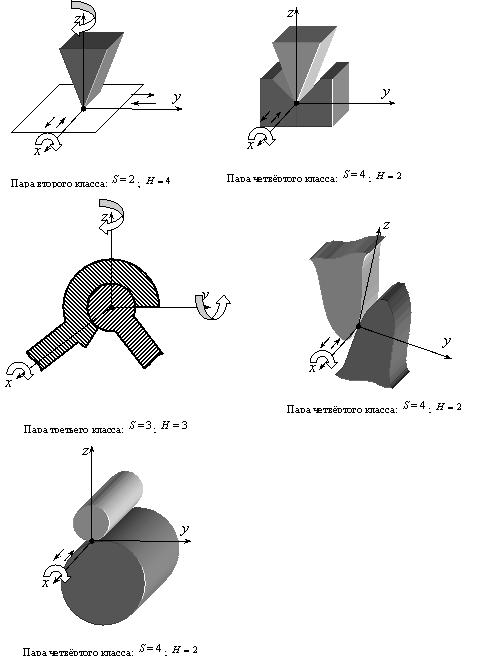
Все пары делятся на пять классов, в зависимости от числа налагаемых связей на подвижность каждого из звеньев. Например, если телами (звеньями), образовавшими кинематическую пару, утрачено по 5 степеней свободы каждым, эту пару называют кинематической парой 5-го класса. Если утрачено 4 степени свободы – 4-го класса и т.д. Число степеней подвижности обозначается за . Число налагаемых связей обозначается за .При этом число степеней подвижности можно определить по формуле: .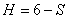

Пара первого класса: ; .

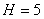Пара второго класса: ; .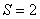

Пара третьего класса: ; .

Пара четвёртого класса: ; .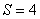

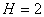Пара пятого класса: ; .

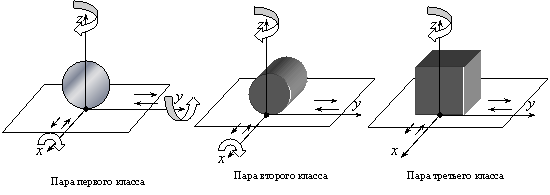
Примеры классификации пар:

Рассмотрим кинематическую пару «винт-гайка» (рис.2.4). Число степеней подвижности этой пары равно 1, а число налагаемых связей равно 5. Это пара будет являться парой пятого класса, свободным можно выбрать только один вид движения для винта или гайки, а второе движение будет сопутствующим.

Рис.2.4

Классификация кинематических цепей

Несколько звеньев, соединённых между собой кинематическими парами, образуют кинематическую цепь.

Кинематические цепи бывают:

- замкнутые (простые). В замкнутой цепи каждое звено входит не менее, чем две кинематические пары.

- разомкнутые (простые).

- сложные.

По признаку наличия разветвлений различают цепи простые (каждое звено цепи входит не более, чем две кинематических пары) и сложные или разветвленные (некоторые звенья входят в три, или более пары); в разветвленных цепях могут присутствовать так называемые кратные (двойные, тройные и т.д.) шарниры.

По области движения звеньев цепи бывают плоские (траектории движения точек всех звеньев - плоские кривые, лежащие в параллельных плоскостях) и пространственные.

Чтобы из кинематической цепи получить механизм, необходимо:

- одно звено сделать неподвижным, т.е. образовать станину (стойку);

- одному или нескольким звеньям задать закон движения (сделать ведущими) таким образом, чтобы все остальные звенья совершали требуемые целесообразные движения.

Некоторые дополнительные определения:

Обобщенная координата механизма – каждая из независимых координат, определяющих положение всех звеньев механизма относительно стойки;

Число степеней свободы механизма – это число степеней свободы всей кинематической цепи относительно неподвижного звена (стойки).

Для пространственной кинематической цепи в общем виде условно обозначим:

- количество подвижных звеньев – n,

- количество степеней свободы всех этих звеньев – 6 n,

- количество кинематических пар 5-го класса – P ₅,

- количество связей, наложенных кинематическими парами 5-го класса на звенья, входящие в них, – 5 Р ₅,

- количество кинематических пар 4-го класса – Р ₄,

- количество связей, наложенных кинематическими парами 4-го класса на звенья, входящие в них, – 4 Р ₄ и т.д.

Звенья кинематической цепи, образуя кинематические пары с другими звеньями, утрачивают часть степеней свободы. Оставшееся число степеней свободы кинематической цепи относительно стойки можно вычислить по формуле

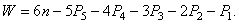
Это структурная формула пространственной кинематической цепи, или формула Малышева, получена П.И. Сомовым в 1887 году и развита А.П. Малышевым в 1923 году.

Величину W называют степенью подвижности механизма (если из кинематической цепи образован механизм).

Для плоской кинематической цепи и соответственно для плоского механизма

Эту формулу называют формулой П.Л. Чебышева (1869). Она может быть получена из формулы Малышева при условии, что на плоскости тело обладает не шестью, а тремя степенями свободы:

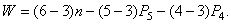
Величина W показывает, сколько должно быть у механизма ведущих звеньев (если W = 1 – одно, W = 2 – два ведущих звена и т.д.).

Дата добавления: 2014-01-05