Бинарные отношения. Основные определения

Бинарным (двухместным) отношением R называется подмножество пар (a, b) Î R прямого произведения М1хМ2 т.е. R ÍМ1 хМ2. При этом множество М1 называют областью определения отношения R, множество М2- областью значений. Часто рассматривают отношения R между парами элементов одного и того же множества М, тогда R Í MxM. Если а, b находятся в отношении R, это часто записывается как а Rb.

Пусть R Í AхВ определено в соответствии с изображением на рис. 1.6. Область определения D(R) и область значений Q(R) определяются соответственно:

D(R) = {а: (а, b) ÎR }, Q(R) = {b: (a, b) Î R}.

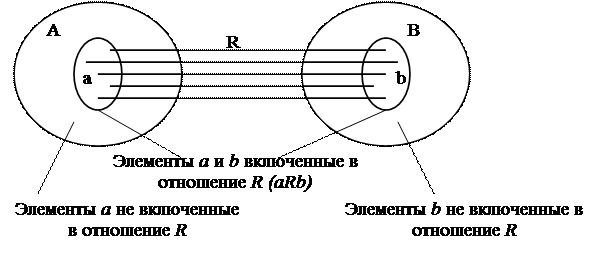Рис. 1.6. Отношение R на множествах А и В

Способы задания бинарных отношений - любые способы задания множеств (так как отношения определены выше как подмножества некоторых множеств - прямых произведений). Отношения, определенные на конечных множествах, обычно задаются:

1. Списком {перечислением) пар, для которых это отношение выполняется (например R = {(d, b), (f, r), (s,d)}.

2. Матрицей - бинарному отношению R Í МхМ, где М= {a₁,a₂..а_п}, соответствует квадратная матрица порядка n, в которой каждый элемент 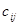определяется следующим образом:

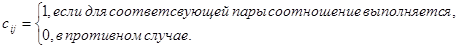
Пример 3 .

Для конечного множества 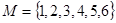задать списком и матрицей отношение R «иметь общий делитель равный двум».

Отношение R содержит все пары элементов (a,b) из M, такие что оба они делятся на 2 без остатка (табл. 1.1). Тогда R={(2,2),(4,2),(6,2),(2,4),(4,4),(6,4),(2,6),(4,6),(6,6)}

Таблица 1.1. Матрица отношения «иметь общий делитель равный двум»

R

Отношение 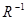называется обратным к отношению 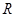, если 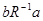тогда и только тогда, когда 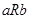. Непосредственно из определения следует, что 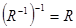. Например, для отношения «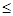» обратным является отношение «».

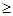Пусть R - отношение на множестве М, RÍМ х М, Тогда:

1) Отношение 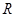называется рефлексивным, если для любого элемента 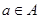имеет место 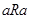. Главная диагональ матрицы рефлексивного отношения содержит только единицы (например отношения «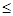» и «иметь общий делитель»).

2) Отношение 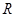называется антирефлексивным, если ни для какого элемента 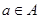не выполняется 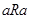. Главная диагональ матрицы антирефлексивного отношения содержит только нули (например отношения «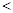» и «иметь сына»).

3) Отношение 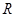называется симметричным, если для любой пары 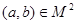из отношения 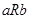следует 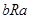. Иными словами, отношение 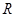является симметричным тогда и только тогда, когда для любой пары 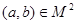оно выполняется в обе стороны (или вовсе не выполняется). Матрица симметричного отношения симметрична относительно главной диагонали: 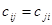для любых 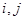. (например отношение «быть симметричным относительно оси абсцисс» является симметричным: если первая точка симметрична второй относительно этой оси, то и вторая точка симметрична первой, «работать на одной фирме»).

4) Отношение 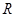называется антисимметричным, если из отношени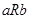й и 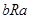следует, что 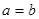. (например отношение «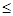» является антисимметричным. Действительно, есл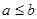и и , это означает, что ).

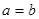5) Отношение 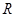называется транзитивным, если для любых 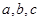из отношени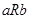й и 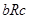следует 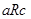. (пример отношения «быть равным», «жить в одном городе», «быть параллельным». Отношение «быть сыном» не является транзитивным).

Замечание. В отличие от отношений рефлексивности и симметричности, для отношения транзитивности не формулируется противоположного понятия (антитранзитивности).

Дата добавления: 2014-01-05