Взаимно однозначные соответствия и мощности множеств

Пример 1.

а) Англо-русский словарь устанавливает соответствие между множествами слов русского и английского языка. Оно не является функциональным, так как почти каждому русскому слову соответствует несколько английских переводов; оно, также, не является, как правило, полностью определённым соответствием, так как всегда существуют английские слова, не включённые в данный словарь. Таким образом, это частичное соответствие.

б) Соответствие между расположенными на шахматной доске фигурами и занимаемыми ими полями является взаимно однозначным.

в) Соответствие между телефонами города и их шестизначными номерами обладает, на первый взгляд, всеми свойствами взаимнооднозначного соответствия. Однако оно, например, не сюръективно, поскольку существуют пятизначные числа, не соответствующие никаким телефонам.

Если между двумя конечными множествами А и В существует взаимнооднозначное соответствие, то эти множества равномощны. Этот очевидный факт позволяет, во-первых, установить равенство мощности этих множеств, не вычисляя их. Во-вторых, часто можно вычислить мощность множества, установив его однозначное соответствие с множеством, мощность которого известна, либо легко вычисляется.

Теорема. Если мощность конечного множества А равна n, то число всех подмножеств А равно 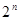, то есть .

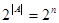Множество А называется счётным множеством, если оно равномощно множеству натуральных чисел : .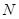

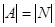Множество N² – счетно.

Доказательство

Разобьем N² на классы

К 1-ому классу отнесем все пары чисел с минимальной суммой N₁ (1;1)

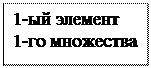Ко 2-му классу отнесем все пары чисел с суммой 3: N₂ {(1;2), (2;1)}

К i-му классу N_i {(a;b)| (a+b=i+1}

Каждый класс будет содержать i пар.

Упорядочим классы по возрастанию индексов i, а пары внутри класса упорядоченные по возрастанию первого элемента а. Занумеруем получившуюся последовательность пар номерами 1,2,3.. Видно, что если a+b=i+1, то пара (a,b) получит номер 1+2+..+(i-1)+. Эта нумерация и доказывает счетность множества N².

Аналогично доказывается счетность множеств N³,…,N^k.

Теорема (теорема Кантора). Множество всех действительных чисел из отрезка 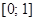не является счётным.

Доказательство. Допустим, что множество 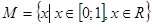является счётным и существует его нумерация. Поскольку любое действительное число можно представить в виде бесконечной десятичной дроби (периодической или непериодической), то проделаем это с числами данного множества. Расположим их в порядке этой нумерации:

Теперь рассмотрим любую бесконечную десятичную дробь вида 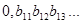, организованную таким образом, что и так далее. Очевидно, что данная дробь не входит в рассматриваемую последовательность, поскольку от первого числа она отличается первой цифрой после запятой, от второго – второй цифрой и так далее. Следовательно, мы получили число из данного интервала, которое не пронумеровано и, таким образом, множество 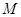не является счётным. Его мощность называется континуум, а множества такой мощности называются континуальными. Приведённый метод доказательства называется диагональным методом Кантора.

Следствие 1. Множество действительных чисел 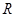континуально.

Следствие 2. Множество всех подмножеств счётного множества континуально.

Дата добавления: 2014-01-05