Операции. Операция - это функция, все аргументы и значения которой принадлежат одному и тому же множеству

Операция - это функция, все аргументы и значения которой принадлежат одному и тому же множеству. В общем случае n- местная функция типа φ:M×M×…×M→M (иное обозначение φ: Mⁿ →M) называется п-арной операцией на множестве M. В таких случаях говорят, что множество M замкнуто относительно операции φ (результат выполнения операции φ на M принадлежит M).

Унарная операция – это функция одного аргумента φ(х) = у, имеющая тип φ: М → M.

Пример 3.

Унарные операции:

• элементные функции е^x, logx, sinx;

• операция над множествами дополнение Ā.

Бинарная операция – это функция двух аргументов φ(х,у)=z, имеющая тип φ: М × М → M.

Пример 4.

Бинарные операции:

• арифметические операции: сложение, вычитание, умножение, деление;

• операции нал множествами: пересечение, объединение, разность;

• операция композиции функций, отображений, отношений.

Если над элементами a,b 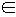М выполняется операция φ, дающая результат z 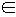М, то это записывается как а φ b = z.

Свойства бинарных операций

1) φ - ассоциативна, если для любых а, b, с из М выполняется

(а φ b) φ с = а φ (b φ с)

Арифметические операции сложения и умножения, операции пересечения и объединения множеств, композиция отображений - ассоциативные операции. Свойства ассоциативности означает, что скобки в выражении аφbφс можно не расставлять;

2) φ- коммутативна, если для любых a, b выполняется

a φ b = b φ a

Арифметические операции сложения и умножения, операции пересечения и объединения множеств - коммутативные операции. Арифметические операции вычитания и деления, операция разности множеств, композиция перестановок и преобразований типа А →А конечного множества – некоммутативны;

3) φ - дистрибутивна слева относительно операции ψ, если для любых a, b, с выполняется

а φ (b ψ с) = (а φ b) ψ (а φ с)

и φ дистрибутивна cправa относительно операции ψ. если для любых a, b, с выполняется

(а ψ b) φ c = (а φ с) ψ (b φ с)

Арифметические операции умножения и деления дистрибутивны относительно операций сложения и вычитания слева и справа, но не наоборот: операции сложения и вычитания недистрибутивны относительно операции умножения и деления: операции объединения и пересечения множеств дистрибутивны относительно друг друга слева и справа.

Способы задания операций.

Так как операция является функцией, то для ее задания применимы любые способы задания функций.

1. Способы задания унарных операций φ: М →М на конечном множестве М= {а₁,а₂,..., а _n}:

• Перечнем всех аргументов а из M (для частично определенной операции - из ее области определения пр₁ φ 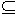М) и соответствующих им значений b, a, b 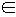M, представленных строкой

φ = (а₁ → b₁, а₂ →b₂,..., а_n →b_n).

В случае, если предварительно зафиксирован список элементов (а₁,а₂,..., а _n ) множества M, то для задания операции φ достаточно указать вектор значений (b₁,b₂,..., b _n ), φ(а_i) = b_i.

• Списком всех пар «аргумент-значение »(а, b) 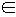φ, a,b 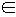M, для всех возможных значений аргументов:

φ= {(a₁, b₁),(a₂, b₂),…,(a_n, b_n)}

• Формулой φ(а) = b.

2. Способы задания бинарных операций φ: М × М → М на конечном множестве М= { а₁,а₂,..., а _n}:

• Таблицей, где слева и сверху таблицы выписываются все значения аргументов а и b из множества M соответственно, а на пересечении строки, соответствующей аргументу а, и столбца, соответствующего аргументу b, записывается результат с операции φ над а и b (табл. 1.2).

Таблица 1.2. Операция умножения на множестве М ={0. 1, 2,3}

*

• Списком всех троек (a, b, с), где а, b соответственно первый и второй аргументы из M, с результат выполнения операции φ над а и b, a, b,с 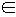M.

• Формулой φ(а, b) = с - - так называемое префиксное представление операции; иное инфиксное - представление бинарной операции формулой а φ b =с.

Дата добавления: 2014-01-05