Алгебра логики. Вопросы для повторения

Тема 2.2. Алгебра логики. Булева алгебра

Резюме по теме

Вопросы для повторения

1.Что называется логической связкой?

2.Дайте определение логической формуле?

3.В чем состоит отличие простой и сложной логической связки?

4.Эквивалентность и равнозначность это одно и то же?

5.Приведите пример дизъюнкции?

6.В чем заключается особенность импликации?

7.Почему некоторые рассуждения являются не правильными?

8.Что изучает раздел математической логики?

Сформировано понятие логической связки. Выделены простые и сложные (составные) связки. Приведены основные виды логических связок. Дано определение логической формуле. Приведены наиболее часто употребляемые схемы логически правильных рассуждений, а так же рассмотрены примеры, в которых используются логически не правильные связки.

Цель: ознакомиться с алгеброй логики и основными понятиями булевой алгебры.

Задачи:

1. Рассмотреть алгебру логики.

2. Ознакомиться с булевой алгеброй.

3. Изучить эквивалентные преобразования.

Алгебра логики как раздел математической логики изучает строение сложных логических высказываний (логических формул) и способы установления их истинности с помощью алгебраических методов.

Объектами, изучаемые в этом разделе являются формулы алгебры логики, состоящие из букв, знаков логических операций и скобок. Буквы обозначают логические (двоичные) переменные, которые принимают только два значения – «ложь» и «истина». Знаки операций обозначают логические операции (логические связки). Каждая формула задает логическую функцию, которая сама может принимать только два логических значения.

Пусть В = {0, 1} - бинарное множество, элементами которого являются формальные символы 1 и 0, интерпретируемые как {истинно, ложно}.

Алгебра логики - алгебра, образованная множеством В = {0, 1} вместе со всеми возможными операциями на нем.

Функция алгебры логики f от n переменных f(х1, х2,..., х_n) называется n -арная логическая операция на В, f:Вn → В.

Любую логическую функцию f(х1, х2,..., х_n) можно задать таблицей истинности, в левой части которой выписаны все возможные наборы значений ее аргументов (х1, х2,..., х_n), а правая часть представляет собой столбец значений функций, соответствующих этим наборам.

Число всех возможных различающихся наборов значений n переменных логической функции f(х1, х2,..., х_n) равно 2ⁿ.

Множество всех логических функций одной переменной (унарные операции) представлено в табл. 2.1. Так как для унарной операции функция применяется к одной переменной находящейся в состоянии либо 0 либо 1, то число всех возможных наборов значений 2¹ равно 2, а следовательно число функций равно 4.

Таблица 2.1. Логические функции одной переменной

х	f0(х)	f1(х)	f2(х)	f3(х)
Результат функции		х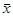
Название функции	Константа 0	Повторение переменной	Отрицание переменной	Константа 1

В случае бинарных операций число всех возможных различающихся функций равно 16. Множество всех логических функций двух переменных (бинарных логических операций) - представлено в табл. 2.2.

Таблица 2.2. Логические функции двух переменных

х1 х2

f0

f1

f2

f3

f4

f5

f6

f7

f8

f9

f10

f11

f12

f13

f14

f15

&

х1

х2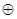

v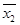

↓

≈

←

→

|

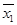
Назовем основные функции из табл. 2.2.

f₀(х₁ х₂) – константа 0;

f₁(х₁ х₂) – конъюнкция;

f₃(х₁ х₂) – переменная х₁;

f₅(х₁ х₂) – переменная х₂;

f₆(х₁ х₂) – сложение по модулю 2;

f₇(х₁ х₂) – дизъюнкция;

f₈(х₁ х₂) – стрелка Пирса;

f₉(х₁ х₂) – эквивалентность;

f₁₀(х₁ х₂) – отрицание х₂;

f₁₂(х₁ х₂) – отрицание х₁;

f₁₃(х₁ х₂) – импликация;

f₁₄(х₁ х₂) – штрих Шеффера;

f₁₅(х₁ х₂) – константа 1.

Формулы называются эквивалентными (равносильными) если они представляют собой одну и ту же функцию.

Метод установления эквивалентности двух формул:

1. по каждой формуле восстанавливается таблица истинности;

2. полученные таблицы сравниваются по каждому набору значений переменных.

Дата добавления: 2014-01-05