Эквивалентные преобразования

Эквивалентные преобразования - преобразования, использующие эквивалентные соотношения и правило замены.

Два правила замены:

1. Правило подстановки формулы f вместо переменной х. При подстановке формулы f вместо переменной х все вхождения переменной х в исходное соотношение должны быть одновременно заменены формулой f.

2. Правило замены подформул. Если какая-либо формула f, описывающая функцию φ, содержит f₁ в качестве подформулы, то замена f₁ на эквивалентную f₂ (f1= f₂) не изменит функции φ.

Основные эквивалентные соотношения (законы) в булевой алгебре.

Ассоциативность конъюнкции и дизъюнкции:
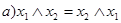
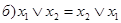
	(1)

Коммутативность конъюнкции и дизъюнкции:
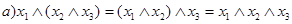
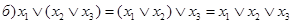
	(2)

Дистрибутивность конъюнкции относительно дизъюнкции:
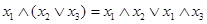
	(3)

Дистрибутивность дизъюнкции относительно конъюнкции:
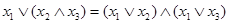
	(4)

Идемпотентность:
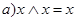
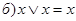
	(5)

Закон двойного отрицания:
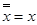
	(6)

Свойства констант 0 и 1:
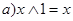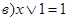
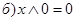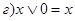
	(7)

Правила де Моргана:
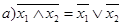
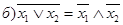
	(8)

Закон противоречия:
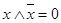
	(9)

Закон исключенного третьего:
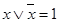
	(10)

Основные эквивалентные соотношения (1) – (10) отличаются тем, что они не выводимы друг из друга и этих соотношений достаточно для выполнения любых эквивалентных преобразований.

Для упрощения формул так же используются следующие эквивалентные соотношения, выводимые из основных с помощью эквивалентных преобразований:

Поглощение:
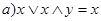
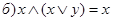
	(11)

Склеивание:
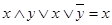
	(12)

Обобщенное склеивание:
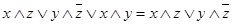
	(13)

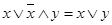
(14)

Приведение к дизъюнктивной нормальной форме.

Элементарная конъюнкция - конъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более одного раза.

Дизъюнктивная нормальная форма (ДНФ) - формула, имеющая вид дизъюнкции элементарных конъюнкций.

Приведении формулы к ДНФ осуществляется в 4 этапа:

1. все отрицания «спустить» до переменных с помощью (6) и (8);

2. раскрыть скобки с помощью (1), (3), (4);

3. удалить лишние конъюнкции и повторения переменных в конъюнкциях с помощью (5), (9), (10);

4. удалить константы с помощью (7).

Процедура приведения ДНФ к СДНФ состоит в расщеплении (использовании (12) в обратную сторону) конъюнкций, которые содержат не все переменные.

Приведение к конъюнктивной нормальной форме.

Элементарная дизъюнкция - дизъюнкция переменных или их отрицаний, в которой каждая переменная встречается не более одного раза.

Конъюнктивная нормальная форма (КНФ) - конъюнкция элементарных дизъюнкций.

Пусть ДНФ F имеет вид F=k₁Úk₂Ú…Úk_m, где k_1,k_2,…,k_m - элементарные конъюнкции. Приведение ДНФ к КНФ состоит из двух шагов:

1. Применить к F правило двойного отрицания 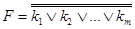и привести 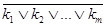к ДНФ k¢₁Ú k¢₂Ú…k¢_p где k¢₁Ú k¢₂Ú…k¢_p - элементарные конъюнкции. Тогда

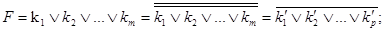
2. С помощью правил де Моргана освободиться от второго отрицания и преобразовать отрицания элементарных конъюнкций в элементарные дизъюнкции D₁,D₂,…D_p Тогда

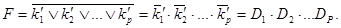
Совершенная КНФ (СКНФ) - КНФ, каждая элементарная дизъюнкция которой содержит все переменные.

Дата добавления: 2014-01-05