Пример 3

Способы задания автоматов

Существуют следующие способы задания абстрактных автоматов: табличный, графический и матричный.

Табличный способы задания автомата

Задание автомата Мили.

Таблица 2. Задание автомата Мили

X S	X1	X2	...	XM
S0	d(S0,X1)/l(S0,X1)	d(S0,X2)/l((S0,X2)	...	d(S0,XM)/l(S0,XM)
S1	d(S1,X1)/l(S1,X1)	d(S1,X2)/l(S1,X2)	...	d(S1,XM)/l(S1,XM
...
SK-1	d(SK-1,X1)/l(SK-1,X1)	d(SK-1,X2)/l(SK-1,X2)	...	d(SK-1,XM)/l(SK-1,XM)

Строкам таблицы 2 соответствуют состояния, столбцам – входные сигналы (буквы). На пересечении i -й строки и j -го столбца записывается состояние, в которое автомат переходит из состояния S_i при подаче на его вход X_j и выходной сигнал Y_p, который вырабатывается при данном переходе.

Иногда автомат задают в виде двух таблиц – таблицы переходов и таблицы выходов. В таблице переходов на пересечении строк и столбцов записываются следующие состояния, в таблице выходов – соответствующие данным переходам выходы.

Задание автомата Мура. В общем случае автомат Мура представлен отмеченной таблицей 3 переходов. Строки таблицы, соответствующие состояниям, отмечены выходными сигналами.

Таблица 3. Задание автомата Мура

Вход Выход	Состояние	X1	X2	...	XM
l(S0)	S0	d(S0 ,X1)	d(S0 ,X2)		d(S0 ,XM)
l(S1)	S1	d(S1,X1)	d(S1,X2)		d(S1 ,XM)
...
l(Sk-1)	Sk-1	d(Sk-1,X1)	d(Sk-1,X2)		d(Sk-1,XM)

Задание автомата в виде ориентированного графа

Задание автомата Мили. Вершинам графа ставятся в соответствие состояния автомата, а ребрам – переходы. Стрелка указывает направление перехода. Вершины отмечаются состояниями; на ребре указывается входной сигнал, вызывающий данный переход, и выходной сигнал, вырабатывающийся при данном переходе.

Пример 2.

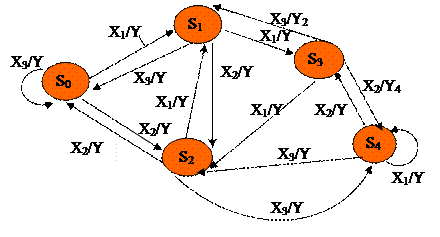X = {X₁, X ₂, X₃ }; Y = { Y₁, Y₂, Y₃, Y₄ }; S = {S₀, S₁, S₂, S₃, S₄}

Рис. 5.4. Граф автомата Мили

Задание автомата Мура. Каждая вершина графа отмечается состоянием и выходным сигналом. На ребре указывается только входной сигнал, вызывающий данный переход.

Рис. 5.5. Граф автомата Мура

Задание автомата в виде матрицы

Автомат задается в виде квадратной матрицы, строки и столбцы которой отмечены состояниями, как показано на табл. 4.

Автомат Мили.

Если из состояния S_i есть переход в состояние S_j под действием сигнала X_k и при этом вырабатывается сигнал Y_P, то на пересечении i -й строки и j -го столбца записываются входной и выходной сигналы X_K/Y_P соответственно.

Пример задания автомата Мили (табл. 4), приведенного на рис. 4.

Таблица 4. Задание матрицей автомата Мили (рис. 4)

	So	S1	S2	S3	S4
So	X3/Y1	X1/Y1	X2/Y2	-	-
S1	X3/Y1	-	X2/Y3	X1/Y2	-
S2	X2/Y4	X3/Y2	-	-	X1/Y3
S3	-	X1/Y2	X1/Y2	-	X2/Y4
S4	-	-	X3/Y1	X2/Y4	X1/Y1

Автомат Мура.

Для задания автомата Мура требуется две матрицы: матрица переходов и вектор выходных сигналов.

Пример задания автомата Мура, приведенного на рис. 5.

Таблица 5. Задание матрицей автомата Мили (рис. 5)

	So	S1	S2
So	-	X1	X2	So	Y1
S1	-	X2	X1	S1	Y2
S2	X1	-	X2	S2	Y1

Другой формой матричного представления автомата являются матрицы переходов. Они описывают, как распределяются переходы для каждого входа отдельно. Каждому входу x ставится в соответствие матрица переходов Т^x=|t^x_{j k}|, в которой для каждого состояния имеется один столбец и одна строка; t^xj_k=1, если вход x переводит автомат из состояния S_j в состояние S_{k ;}; t^xj_k=0, если вход x переводит автомат из S_j в S_p (p = k).

Построим граф переходов детектора входных последовательностей нулей и единиц. Если на вход автомата поступает последовательность из четырех единиц, то на выходе автомата появляется “1”. Во всех остальных ситуациях на выходе автомата – “0”.

X = {0, 1}; Y = {0, 1}. Множество состояний, функцию переходов и функцию выходов определим при построении графа (рис. 5.6). S = {S₀, S₁, S₂, S₃}.

Состояние S₀ является начальным и хранит информацию о том, что последний входной сигнал был нулем. Состояние S₁ хранит информацию о том, что на вход детектора была подана одна единица, S₂ – о том, что на входе две единицы, S₃ помнит предысторию трех единиц.

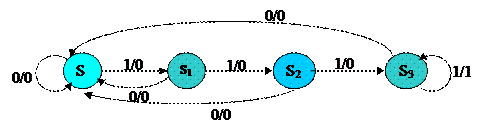
Рис. 5.6. Автомат детектора входных последовательностей нулей и единиц

Дата добавления: 2014-01-05