Расчет тарифа в массовых видах рискового страхования

Нагр

Задача неразорения страховщика

Классификация и оценка рисков

При разумном поведении человек не ставит задачу извлечь выгоду из неблагопри­ятного случая. Поэтому страховщик, принимая на себя риски страхователя не из альтру­изма, а за плату, должен прежде оценить их тяжесть и способы его обеспечения по его удовлетворению. С точки зрения природы и последствий рисков их можно разделить на три основные группы:

1) опасные события, случайные по времени появления на множестве отдельных од­нородных распределенных объектов и размеру причиняемых этим объектам, по отдельности, убытков (пожары, аварии, кражи, травмы и т.п., характерные для массового страхования однородных объектов - домов, автомобилей и т.д.);

2) редкие опасные события, случайные по времени появления и с высоким уровнем убытков, причиняемых сразу множеству компактно расположенных отдельных объектов (катастрофические события);

3) опасные события, о которых известно, что они заведомо произойдут, но неизвест­но, в какое время и с кем (утрата трудоспособности по старости, смерть).

Для оценки этих групп рисков используются различные методы. При этом слу­чайный характер последствий наступления опасных событий может быть количественно оценен, например, исходя из статистических наблюдений за ними. Тогда мы говорим о вероятностном, исчисляемом характере случайного опасного события или риска. Если мы не можем количественно оценить риски, что характерно для редких катастрофиче­ских событий, то говорим о неопределенности риска.

Страхование имеет дело со случайными и исчисляемыми, вероятностными риска­ми. Если риск не определен, то для раскрытия неопределенности можно применить из­вестные методы теории «игр с природой», базирующиеся, вообще говоря, на описанном выше подходе Паскаля. Подобное раскрытие неопределенности не дает количественных оценок вероятности того или иного исхода проявления риска, однако позволяет выявить предпочтительные по заранее выбранному критерию варианты действий по защите от риска. В качестве критериев могут быть рекомендованы максиминный критерий Вальда, предполагающий выбор варианта действий, обеспечивающего максимальный результат в наихудших из возможных условий или критерий Сэвиджа, предполагающий выбор ва­рианта, обеспечивающего минимальный риск в наихудших из возможных условий.

Если страховщик имеет дело с массовыми рисками, то, согласно закону больших чисел, распределение суммарного по всему страховому портфелю убытка будет подчи­няться нормальному распределению независимо от распределения убытков по единич­ным рискам.

Для оценки «качества» или степени риска с точки зрения страхования используют коэффициент вариации, равный отношению среднего квадратического отклонения ве­личины суммарного убытка по страховому портфелю к математическому ожиданию это­го убытка. Такой подход, в частности, предложен К. Бурроу. Если портфель однороден, т.е. случайные величины убытков по единичным рискам распределены одинаково, то при увеличении объема договоров в n раз коэффициент вариации уменьшается в √ n раз. Поэтому достаточно рассмотреть ситуацию для одного договора страхования.

Пусть р вероятность наступления страхового случая с убытком и, величина кото­рого распределена по известному закону. Это позволяет рассчитать условные математи­ческое ожидание М(u|А) и дисперсию D(u| А) убытка, а затем на их основе полные ха­рактеристики М(и) и D(u).

M(u) = M(u|А)*p;

D(u) = D(u|А)*p + p(l-p)*[M(u|А)²]

Это позволяет оценить степень риска:

µ(u)=σ(u)/M(u)

Введем условное математическое ожидание убытка под знак квадратного корня и после несложных преобразований получим выражение:

µ(u)=√(µ(u|А)²) /р + (1-р) /р)

Проанализируем его. Если величина убытка при наступлении страхового случая известна фиксирована, то D(u|А) = 0 и µ(u)=)=√(1-р) /р, откуда следует, что в случае принятия на страхование редких событий, имеющих малую вероятность р, высока сте­пень риска для страховщика получить страховой случай с большой выплатой, особенно если при этом велика страховая сумма.

Таким образом и получен известный коэффициент В.С. Коньшина, оценивающий финансовую надежность страхования:

K=√((1-t)/n*t),

где:

n - число застрахованных объектов;

t - средний тариф по объектам.

Чем ниже величина коэффициента К, тем надежнее страхование. Если величина убытка при страховом случае распределена случайным образом, то степень риска для страховщика величивается за счет дисперсии (разброса) D(u | А) величины убытка. Это делает необходимым увеличивать рисковую надбавку к нетто-величине тарифа

t = M(u) * p / s,

где

s - страховая сумма.

На рис. 3.1 показаны зоны ответственности различных факторов в обеспечении финансовой надежности страховщика.

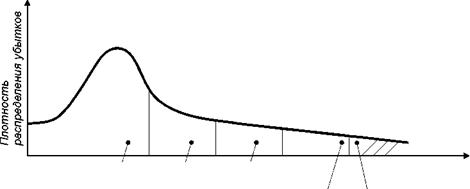
Необеспе- U ченный риск

Основная часть /Рисковая /Перестра- /Собственный нетто-премии /надбавка /хование /капитал

Рис. 3.1. Плотность распределения убытков и области их защиты

Порядок расположения областей показывает последовательность действий стра­ховщика по защите своего портфеля.

При разумном поведении человек не ставит задачу извлечь выгоду из неблагопри­ятного случая. Поэтому страховщик, принимая на себя риски страхователя не из альтру­изма, а за плату, должен прежде оценить их тяжесть и способы его обеспечения по его удовлетворению, чтобы назначить адекватную им стоимость. Тогда условие не разорения страховщика по виду страхования в каждый момент времени t (текущее не разорение) можно записать в виде:

Vct < Uct + РВД вид t + ∆R вид t,

где: Vct - суммарная текущая премия по виду страхования;

U_ct - суммарный текущий убыток по виду страхования;

РВД _вид _t - текущие расходы на ведение дела страховщика, алоцированные на вид страхования;

A R _вид t - текущее приращение страховых резервов по виду страхования.

Если условие неразорения рассматривать за период действия договоров страхова­ния, например, за год, то страховые резервы, по окончанию сроков действия договоров, преобразуются либо в страховые выплаты (суммарный убыток), либо в доходы страхов­щика. Тогда условие неразорения можно записать в виде:

Vc _с< Uc + РВДвид

Перейдя к равенству и разделив обе части на суммарный убыток, получим извест­ное выражение для расчета минимальной величины страхового тарифа T:

T = T_o + T_р + T

где: T_o - основная часть нетто-тарифа, соответствующая математическому ожиданию суммарного убытка;

T_р - рисковая часть нетто-тарифа, соответствующая возможным отклонениям сум­марного убытка в большую сторону относительно его математического ожидания;

T _нагр - часть тарифа, учитывающая расходы на ведение дела страховщика (нагрузка).

С точки зрения методов расчета тарифов страховые риски можно разделить на три основные группы:

1) опасные события, случайные по времени появления на множестве отдельных однородных распределенных объектов и размеру причиняемых этим объектам, по от­дельности, убытков (пожары, аварии, кражи, травмы и т.п.), характерные для массового страхования однородных предметов - домов, автомобилей и т.д.;

2) редкие опасные события, случайные по времени появления и с высоким уров­нем убытков, причиняемых сразу множеству компактно расположенных отдельных предметов (катастрофические события);

3) опасные события, о которых известно, что они заведомо произойдут, но неиз­вестно, в какое время и с кем (утрата трудоспособности по старости, смерть).

Если страховщик имеет дело с массовыми рисками, то, согласно центральной пре­дельной теореме, распределение суммарного по всему страховому портфелю убытка бу­дет подчиняться нормальному распределению независимо от распределения убытков по единичным рискам (рис. 3.2).

Из рис. 3.2 данных видно, что вероятность случайного события «фактическое зна­чение случайной величины суммарного убытка превзошло его математическое ожидание» равна 0,5. Следовательно, при назначении страхового тарифа исходя из математического ожидания суммарного убытка, с такой же вероятностью может возникнуть нехватка соб­ранной страховой премии на выплаты - неплатежеспособность страховщика. Поэтому та­риф рассчитывают исходя из такого значения случайной величины суммарного убытка, которая соответствует некоторому заданному значению доверительной вероятности, на­пример, 0,99. При этом риск неплатежеспособности снижается с 0,5 до 0,01. Чем больше ко­личество принятых на страхование однородных (гомогенных) рисков, тем меньше диспер­сия, и круче наклон кривой, что обеспечивает меньшее значение случайного суммарного убытка и, соответственно, тарифа при заданной доверительной вероятности.

Правильный выбор значения доверительной вероятности - это не только наука, но и интуиция, искусство управления риском страховщика, поскольку снижение риска неплатежеспособности сопровождается повышением цены страховой услуги и снижени­ем объема их продаж.

К рисковым видам страхования, согласно «Методике расчета тарифных ставок по рисковым видам страхования», относятся виды страхования иные, чем страхование жиз­ни, а именно:

• не предусматривающие обязательств страховщика по выплате страховой суммы при окончании срока действия договора страхования;

• не связанные с накоплением страховой суммы в течение срока действия договора страхования.

В свою очередь, из числа рисковых видов страхования выделяют:

• массовые рисковые виды страхования;

• страхование редких событий и крупных рисков;

• медицинское страхование.

Массовые виды страхования охватывают значительное число страхователей и объектов страхования (обычно личное и имущественное страхование, а также страхова­ние ответственности частных лиц и мелких предпринимателей), характеризующихся од­нородностью рисков, для которых существует достаточно большой объем статистических данных (число объектов страхования n не менее нескольких тысяч), позволяющий объек­тивно рассчитать тарифы. Случайное распределение величины убытка в массовых видах с достаточной точностью может быть описано нормальным или логарифмически нор­мальным распределением, что значительно упрощает статистические расчеты.

F(U_C) = P(U_C < U)

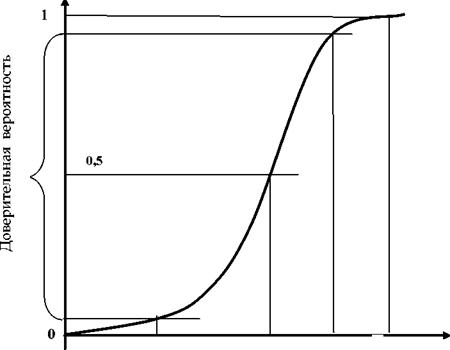Uc тариф Uc max

Рис.3.2. Интегральный закон распределения суммарного убытка и расчет тарифа.

Расчет страхового взноса по рисковому виду страхования включает:

• сбор статистического материала по объектам страхования и произошедшим стра­ховым случаям за прошлый (так называемый расчетный или тарифный) период и проверка его однородности для включения в одну тарифную группу договоров (объектов страхования);

• определение частоты p страхового события как частного от деления числа страхо­вых событий m (например, числа пожаров) на общее число объектов страхования n (например, число застрахованных строений) для тарифной группы;

• определение математического ожидания М (и) и среднего квадратического откло­нения величины страхового убытка (страховой выплаты) σ(u) в страховых случаях и средней страховой суммы на один договор страхования s для вида страхования (тарифной группы) в соответствии с формулами из любого учебника статистики;

• расчет основной части Т₀ нетто-взноса;

• расчет рисковой надбавки Т_р;

• расчет нетто-взноса как суммы основной части и рисковой надбавки;

• расчет брутто-взноса Т _б как суммы нетто-взноса и нагрузки Т_н, учитывающей рас­ходы на ведение дела страховой компании, приходящиеся на один договор.

Согласно «Методике расчета тарифных ставок по рисковым видам страхования», утвержденной распоряжением страхового надзора от 08.07.93 № 02-03-36, основная часть нетто-тарифа Т_о:

M (u)

T_o=p* —---

s

Отсюда следует, что основная часть страхового нетто-тарифа (нетто-ставка) про­порциональна частоте возникновения убытков (страховых случаев).

При известной величине а (и) и для однородных рисков величина рисковой над­бавки определяется по формуле:

Tр=To*α(γ)*√ 1/n{1-p+(σ(u)/s)

где α(γ)- коэффициент, зависящий от выбранного значения доверительной вероятности γ, (табл. 3.2).

Таблица 3.2.

γ	0,84	0,90	0,95	0,95	0,9986
α(γ)	1.0	1.3	1.645	2.0	3.0

В данном случае доверительная вероятность является вероятностью, с которой страховые убытки в прогнозируемом периоде будут меньше, чем прогнозируемые стра­ховые взносы или, другими словами, страховая компания не разорится в прогнозируемом периоде.

Если величины u и σ(u) неизвестны, то рисковую надбавку можно приближенно рассчитать по следующей формуле:

Tр=1,2*To*α(γ)*√ (1-p)/n*p

При расчетах для нескольких видов страхования рисковая надбавка может быть рассчитана пропорционально моментам распределения случайной функции убытка од­ним из следующих методов:

• пропорционально математическому ожиданию

Тр = а * u, (а>0);

• пропорционально среднему квадратическому отклонению

Т_р = b * σ(u), (b>0);

• пропорционально коэффициенту вариации µ (u)

Т_р = с * µ (u), (с>0).

Коэффициент вариации определяется как отношение среднего квадратического отклонения к математическому ожиданию.

Наиболее часто используют среднее квадратическое отклонение. На практике, принимая, например, b = 1-2, получаем величину доверительной вероятности в пределах 96-98%. Дальнейшее увеличение рисковой надбавки и, соответственно, всего страхового взноса может привести к снижению конкурентоспособности.

При медицинском страховании под страховым случаем обычно понимается обра­щение к врачу. Для большинства программ медицинского страхования, предлагаемых страховщиками, таких обращений может быть несколько, поэтому о вероятности наступ­ления страхового случая говорить не приходится. Основную часть нетто-взноса в этом слу­чае определяют как произведение среднего (математического ожидания) количества об­ращений к врачу на среднюю стоимость одного обращения для данной половозрастной группы застрахованных, а рисковую добавку рассчитывают, как показано в разделе 3.1. В связи с особенностями расчета основной части нетто-взноса тариф в медицинском стра­ховании выше, чем в других рисковых видах.

Дата добавления: 2014-01-05