Правило №2. Если А и В два независимых события, то вероятность того, что произойдут оба этих события называется вероятностью их совместного появления

Правило №1. Вероятность полной группы несовместимых событий равна 1.

ПРАВИЛА ТЕОРИИ ВЕРЯТНОСТИ

События называются независимыми, если одно событие может происходить независимо от другого. Независимые события являются совместимыми.

Два и более несовместимых события образуют полную группу событий, если в результате опыта обязательно должно произойти, хотя бы одно из них.

События называются совместимыми, если они могут появиться одновременно.

События называются несовместимыми, если они не могут появиться одновременно.

Пример 1. Опыт с монетой. Обязательно должно произойти хотя бы одно из двух событий – монета упадет гербом или цифрой. Полную группу событий составляет два несовместимых события – событие выпадения монеты гербом и событие выпадения монеты цифрой.

Пример 2. Опыт с кубиком. Кубик имеет 6 граней оцифрованных от 1 до 6. При бросании кубика обязательно должно произойти хотя бы одно из 6 событий - выпадет цифра от 1 до 6. Полную группу событий составляет 6 несовместимых событий выпадение одной из цифр от 1 до 6.

Пример 3. Опыт с двумя кубиками. При бросании сразу двух кубиков одинаковая цифра может появиться одновременно на обоих кубиках. Появление одинаковых цифр на обоих кубиках является двумя независимыми совместимыми событиями.

Два несовместимых события А и В составляют полную группу событий. Если Р(А) вероятность появления события А, а Р(В) вероятность его не появления то:

Р(А) + Р (В) = 1.

Пример 4. Обозначим вероятность события выпадения монеты цифрой Р(А), а вероятность события выпадения монеты гербом Р(В). События выпадения монеты цифрой или гербом равновероятны: Р(А) = Р(В) = 0,5. Следовательно, выполняется условие:

Р(А) + Р(В) = 0,5 + 0,5 = 1.

Вероятность появления двух независимых событий равна произведению вероятностей этих событий:

Р(А и В) = Р(АВ) = Р(А)·Р(В).

Пример 5. Бросили 2 монеты. Определить вероятность выпадения цифр на двух монетах.

Решение. Вероятность выпадения цифры на первой монете (появление события А) составляет Р(А) = 0,5. Вероятность выпадения цифры на второй монете (появление события В) составляет Р(В) = 0,5. Вероятность совместного появления двух независимых событий составляет Р(А и В) = Р(АВ) = Р(А) ·Р(В) = 0,5 · 0,5 = 0,25.

Правило №3. Вероятность совместного появления каждого из N независимых событий А₁, А₂, А₃, … Аn равна произведению вероятностей появления каждого из этих событий в отдельности:

Р (А₁ и А₂ и А₃ и… Аn) = .

Пример. Бросили 3 монеты. Определить вероятность того, что все три упали гербом.

Решение. Вероятность выпадения орла на каждой из монет одинакова и составляет Р(А₁) = Р(А₂) = Р(А₃) = 0,5. Вероятность совместного появления трех этих событий Р (А₁ и А₂ и А₃) = = 0,5 ·0,5 · 0,5 = 0,125.

Проверка. Полная группа событий выпадения трех монет гербами или цифрами составит 8 возможных сочетаний:

ГГГ; ГГЦ; ГЦ Г; ГЦЦ; ЦЦЦ; ЦЦГ; ЦГЦ; ЦЦГ.

Тогда вероятность выпадения одного из этих сочетаний составит 1 / 8 = 0,125.

Правило №4. Если А и В – два несовместимых события, то вероятность того, что произойдет одно из них равна сумме вероятностей появления каждого из этих событий:

Р(А или В) = Р(А) + Р(В).

Пример 6. Опыт с монетой. Появление герба (событие А) и цифры (событие В) являются двумя несовместимыми событиями. Найти вероятность того, что произойдет одно из этих событий.

Решение. Появления герба (событие А) и цифры (событие В) являются равновероятными событиями. Вероятность события А составляет Р(А) = 0,5. Вероятность события В составляет Р(В) = 1 – Р(А) = 0,5. Тогда Р(А или В) = 0,5 + 0,5 = 1.

Пример 7. Бросили шестигранный кубик. Определить вероятность выпадения цифры 1 или цифры 2.

Решение. Выпадение цифры 1 (событие А) и выпадение цифры 2 (событие В) представляют собой равновероятные несовместимые события: Р(А) = Р(В) = 1/6. Тогда вероятность Р(А или В) = Р(А) + Р(В) = 1/6 + 1/6 = 1/3.

Правило №5. Вероятность появления любого одного события А₁ или А₂ или А₃ или … Аn из N несовместных событий равна сумма вероятностей этих событий:

Р(А₁ или А₂ или А₃ или … Аn) =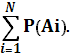

Пример. Опыт с кубиком. Бросили кубик. Определить вероятность появления любой цифры от 1 до 5.

Решение. Выпадение любой цифры от 1 до 5 (событие Аi) представляет собой равновероятное несовместное событие, т.е. Р(Аi) = 1/6. Тогда вероятность появления любой цифры от 1 до 5 определится как:

Р(А₁ или А₂ или А₃ или А₄ или А₅) = 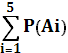= 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 5/6.

Правило №6. Если А и В два независимых события, то вероятность того, что произойдет одно из этих событий определяется, как:

Р(А или В) = Р(А) + Р(В) – Р(АВ) = Р(А) + Р(В) – Р(А) · Р(В).

Пример 8. Бросаем 2 монеты. Определить вероятность того, что на одной из двух монет выпадет орел.

Решение. Событие А выпадение орла на первой монете имеет вероятность Р(А) = 0,5. Событие В выпадения орла на второй монете имеет вероятность Р(В) = 0,5. Тогда вероятность того, что орел выпадет на одной из двух монет, составит:

Р(А или В) = Р(А) + Р(В) – Р(АВ) = Р(А) + Р(В) – Р(А) · Р(В) = 0,5 + 0,5 – 0,5 · 0,5 = 0,75.

Правило №7. Если А и В два совместных события, то условная вероятность Р(В/А) появления события В при появлении события А определяется как:

Р(В/А) = Р(АВ) / Р(А).

Правило №7 связывает между собой появление двух случайных совместных событий. Данное правило используется при определении надежности объектов со сложными структурными схемами.

Задача. При изготовлениитранзисторных усилителей используются транзисторы, поступающие от поставщика №1 и поставщика №2. 75% транзисторов поступает от поставщика №1 и 25% транзисторов поступает от поставщика №2. 99% транзисторов поставщика № 1 исправны. 90% транзисторов от поставщика №2 исправны.

Определить:

1. Какова вероятность того, что любой случайно взятый транзистор окажется исправным транзистором от поставщика №1?

2. Какова вероятность того, что любой случайно взятый транзистор окажется неисправным транзистором от поставщика №1?

3. Какова вероятность того, что любой случайно взятый транзистор окажется исправным транзистором от поставщика №2?

4. Какова вероятность того, что любой случайно взятый транзистор окажется неисправным транзистором от поставщика №2?

5. Какова вероятность того, что любой случайно взятый транзистор окажется исправным не зависимо от его поставщика?

6. Какова вероятность того, что любой случайно взятый транзистор окажется неисправным не зависимо от его поставщика?

Решение. Событие «транзистор от поставщика №1 обозначим как А₁, а Событие «транзистор от поставщика №2 обозначим как А₂»_. Событие «исправный транзистор» обозначим как В₁, а событие «неисправный транзистор» обозначим как В₂.

Тогда:

- событие «исправный транзистор от поставщика №1» запишется, как В₁А₁;

- событие «неисправный транзистор от поставщика №1» запишется, как В₂А₁;

- событие «исправный транзистор от поставщика №2» запишется, как В₁А₂;

- событие «неисправный транзистор от поставщика №2» запишется, как В₂А₂.

- событие «исправный транзистор независимо от поставщика» запишется как В₁;

- событие «неисправный транзистор независимо от поставщика» запишется как В₂.

Определим вероятности первых четырех событий.

Р(В₁А₁) = Р(В₁) · (А₁) = 0,99 · 0,75 = 0,7425.

Любой взятый транзистор окажется исправным транзистором от поставщика №1 с вероятностью 0,7425.

Р(В₂А₁) = Р(В₂) · (А₁) = 0,01 · 0,75 = 0,0075.

Любой взятый транзистор окажется неисправным транзистором от поставщика №1 с вероятностью 0,0075.

Р(В₁А₂) = Р(В₁) · (А₂) = 0,9 · 0,25 = 0,225.

Любой взятый транзистор окажется исправным транзистором от поставщика №2 с вероятностью 0,225.

Р(В₂А₂) = Р(В₂) · (А₂) = 0,1· 0,25 = 0,025.

Любой взятый транзистор окажется неисправным транзистором от поставщика №2 с вероятностью 0,025.

Проверка: Все перечисленные выше события составляют полную группу событий, т.к. других событий быть не может. Вероятность полной группы событий равна единице, следовательно, должно выполняться условие:

Р(В₁А₁) + Р(В₂А₁) + Р(В₁А₂) + Р(В₂А₂) = 1.

Проверим выполнение этого условия в нашем случае:

Р(В₁А₁) + Р(В₂А₁) + Р(В₁А₂) + Р(В₂А₂) = 0,7425 + 0,0075 + 0,225 + 0,025=1.

Условия соблюдается, поэтому вероятность всех событий была определена правильно.

Определим вероятности последних двух событий.

Р(В₁) = Р(В₁А₁) + Р(В₁А₂) = 0,7425 + 0,225 = 0,9675.

Любой взятый транзистор окажется исправным независимо от поставщика с вероятностью 0,9675.

Р(В₂) = Р(В₂А₁) + Р(В₂А₂) = 0,0075 + 0,025 = 0,0325.

Любой взятый транзистор окажется неисправным независимо от поставщика с вероятностью 0,0325.

Проверка: Все перечисленные выше события составляют полную группу событий, т.к. других событий быть не может. Вероятность полной группы событий равна единице, следовательно, должно выполняться условие:

Р(В₁) + Р(В₂) = 1.

Проверим выполнение этого условия в нашем случае:

Р(В₁) + Р(В₂) = 0,9675 + 0,0325 = 1.

Условия соблюдается, поэтому вероятность всех событий была определена правильно.

ЗАКЛЮЧЕНИЕ

1. Выводы по материалу занятия.

2. Ответы на вопросы.

3. Задание на самостоятельную работу.

ЛИТЕРАТУРА

1. Надежность и диагностика систем электроснабжения железных дорог: Учебник для вузов ж/д транспорта/ А.В. Ефимов, А.Г. Галкин. – М.: УМК МПС России, 2000.

Дата добавления: 2014-01-05