ЛЕКЦИЯ №9

СТРУКТУРНАЯ СХЕМА НАДЕЖНОСТИ СИСТЕМ ЭЛЕКТРОСНАБЖЕНИЯ С КОМБИНИРОВАННЫМ РЕЗЕРВИРОВАНИЕМ

СТРУКТУРНАЯ СХЕМА НАДЕЖНОСТИ СИСТЕМ ЭЛЕКТРОСНАБЖЕНИЯ С РАЗДЕЛЬНЫМ РЕЗЕРВИРОВАНИЕМ

СТРУКТУРНАЯ СХЕМА НАДЕЖНОСТИ СИСТЕМ ЭЛЕКТРОСНАБЖЕНИЯ С ОБЩИМ РЕЗЕРВИРОВАНИЕМ

По способу включения резервных устройств резервирование может быть постоянным и с замещением.

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ

Начиная рассматривать данный вопрос, необходимо вспомнить некоторые определения [1]:

Резервированием называется повышение надежности системы, путем включение в ее состав резервных единиц.

Резервирование бывает трех видов – общее, раздельное и смешанное.

Общим называется резервирование, при котором параллельно друг другу включаются идентичные элементы (объекты).

Раздельным называется резервирование системы путем использования отдельных резервных элементов.

Комбинированным называетсясочетание общего и раздельного резервирование в одной системе.

Отношение числа резервных объектов к числу основных называется кратностью резервирования. Кратность резервирования может быть либо целым, либо дробным числом.

Постоянным называется резервирование, при котором резервные элементы соединены с основными элементами в течение всего времени работы.

Замещением называется резервирование, при котором резервные элементы соединяются с основными элементами после их отказа.

Резервные объекты могут находиться в трех режимах работы:

- в нагруженном режиме, при котором резервные элементы находятся в тех же рабочих условиях, что и основные;

- в ненагруженном режиме, при котором резервные элементы не включены в работу;

- в облегченном режиме, при котором резервные элементы включены, но работают не на полную нагрузку.

Рассмотрим схему с последовательным соединением элементов (рисунок 1):

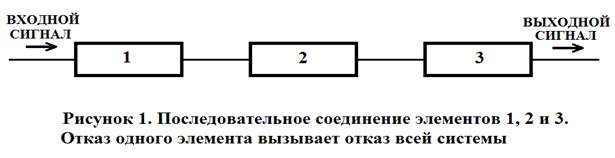
Предположим, что система состоит из трех одинаковых по надежности элементов с вероятностью безотказной работы в течение времени t: Р₁(t) = Р₂(t) = Р₃(t) = 0,997. Тогда вероятность безотказной работы системы Р_с(t) определится, как:

Р_с(t) = Р₁(t) · Р₂(t) · Р₃(t) = { Р (t) }³ = 0,997³ = 0,991027.

Мы считаем, что такая надежность не соответствует требуемой надежности современных систем ЭСЖТ и ее необходимо повысить [2]. Но, предположим, что использовать более надежные элементы нельзя. Либо их нет, либо они очень дороги. Тогда надежность системы может быть повышена путем ее общего резервирования.

Общим называется резервирование, при котором параллельно друг другу включаются идентичные элементы.

Схема системы с постоянным общим резервированием элементов представлена на рисунке 2.

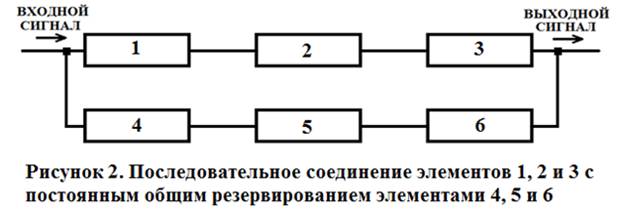
Предположим, что система состоит из 6 одинаковых по надежности элементов с вероятностью безотказной работы в течение времени t: Р₁(t) = Р₂(t) = Р₃(t) = Р₄(t) = Р₅(t) = Р₆(t) = 0,997. Вероятность безотказной работы системы определится, как:

Р_с(t) = 1 – {1 - Р_I(t) } · {1 - Р_II(t) },

где Р_I(t) = { Р (t) }³ = 0,997³ = 0,991027; Р_II(t) = { Р (t) }³ = 0,997³ = 0,991027.

Тогда:

Р_с(t) = 1 – {1 - Р_I(t) } · {1 - Р_II(t) } = 1 – (1 – 0,991027) · (1 – 0,991027) = 1 – (0,008973)² = 1 – 0,0000805 = 0,9999195.

Таким образом, путем общего резервирования система, состоящая из элементов со сравнительно невысокой надежностью, превратилась в близкую к абсолютно надежной систему.

Рассмотренная система называется системой с постоянным общим резервированием, поскольку резервные элементы соединены с основными элементами в течение всего времени работы. Это является недостатком, ведущим к излишнему расходу ресурса работы элементов. Для повышения экономичности расхода ресурса элементов применяются системы с резервированием замещением. В этом случае резервирование включается при отказе основной цепи элементов (рисунок 3).

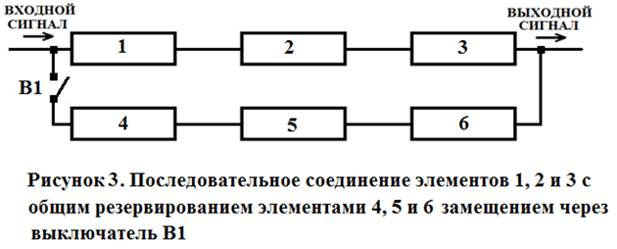
Однако, при наличии выключателя В1 надежность системы снижается, поскольку в схеме появляется еще один элемент. Так, если вероятность безотказной работы выключателя В1 обозначить как Р₇(t) = 0,997, то вероятность безотказной работы системы составит:

Р_с(t) = 1 – {1 - Р_I(t) } · {1 - Р_II(t) } = 1 – (1 – 0,991027) · (1 – 0,991027·0,997) = 1 – 0,008973·0,011946 = 1 – 0,0001072 = 0,999893.

Раздельным называется резервирование системы путем использования отдельных резервных элементов.

Рассмотрим схему с последовательным соединением элементов, представленную на рисунке 1. Элементы одинаковые по надежности Р₁(t) = Р₂(t) = Р₃(t) = 0,997. Рассмотрим схему с раздельным постоянным резервированием (рисунок 4). Система состоит из 6 одинаковых по надежности элементов с вероятностью безотказной работы в течение времени t: Р₁(t) = Р₂(t) = Р₃(t) = Р₄(t) = Р₅(t) = Р₆(t) = 0,997.

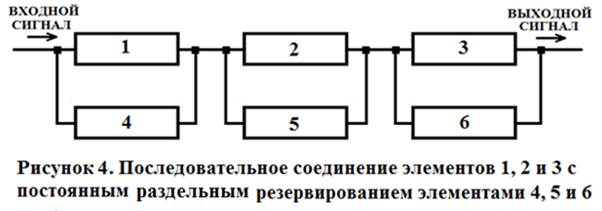
Вероятность безотказной работы системы определится, как:

Р_с(t) = Р_I(t) · Р_II(t) · Р_III(t),

где: - Р_I(t) = 1 – {1 - (Р₁(t) }{1 - (Р₄(t) } = 1 - 0,003² = 0,999991;

- Р_II(t) = 1 – {1 - (Р₂(t) }{1 - (Р₅(t) } = 1 - 0,003² = 0,999991;

- Р_III(t) = 1 – {1 - (Р₃(t) }{1 - (Р₆(t) } = 1 - 0,003² = 0,999991.

Тогда:

Р_с(t) = Р_I(t) · Р_II(t) · Р_III(t) = 0,999991· 0,999991· 0,999991= 0,999973.

Сравним результаты общего и раздельного постоянного резервирования (рисунок 2 и рисунок 4). При общем постоянном резервировании вероятность безотказной работы системы составит Р_с(t) = 0,9999195. При раздельном постоянном резервировании вероятность безотказной работы системы составит Р_с(t) = 0,999973. Таким образом, система с раздельным резервированием является более надежной.

Рассмотрим раздельное резервирование замещением (рисунок 5).

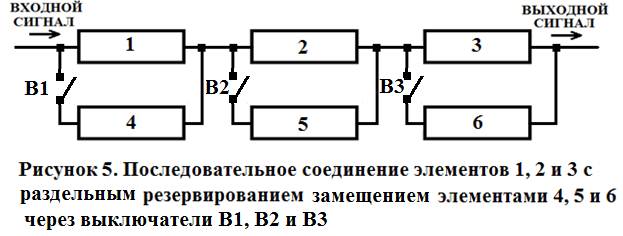
Вероятность безотказной работы выключателей В 1, В2 и В3 обозначить как Р₇(t), Р₈(t), Р₉(t), и примем одинаковой Р₇(t) = Р₈(t) = Р₉(t) = 0,997.

Вероятность безотказной работы системы составит:

Р_с(t) = Р_I(t) · Р_II(t) · Р_III(t),

где - Р_I(t) = 1 – {1 - (Р₁(t) }{1 - (Р₄(t)· (Р₇(t) } = 1 - 0,003·0,00599 = 0,999982;

- Р_II(t) = 1 – {1 - (Р₂(t) }{1 - (Р₅(t)· (Р₈(t) } = 1 - 0,003·0,00599 = 0,999982;

- Р_III(t) = 1 – {1 - (Р₃(t) }{1 - (Р₆(t)· (Р₉(t) } = 1 - 0,003·0,00599 = 0,999982.

Тогда:

Р_с(t) = Р_I(t) · Р_II(t) · Р_III(t) = 0,999982· 0,999982· 0,999982= 0,999946.

Сравним результаты общего и раздельного резервирования замещением (рисунок 3 и рисунок 5). При общем резервировании замещением вероятность безотказной работы системы составит Р_с(t) = 0,999893. При раздельном резервировании замещением вероятность безотказной работы системы составит Р_с(t) = 0,999946. Таким образом, система с раздельным резервированием является более надежной.

Комбинированным называетсясочетание общего и раздельного резервирование в одной системе.

Рассмотрим схему с комбинированным постоянным резервированием (рисунок 6). Система состоит из 9 одинаковых по надежности элементов с вероятностью безотказной работы в течение времени t: Р₁(t) = Р₂(t) = Р₃(t) = Р₄(t) = Р₅(t) = Р₆(t) = Р₇(t) = Р₈(t) = Р₉(t) = 0,997.

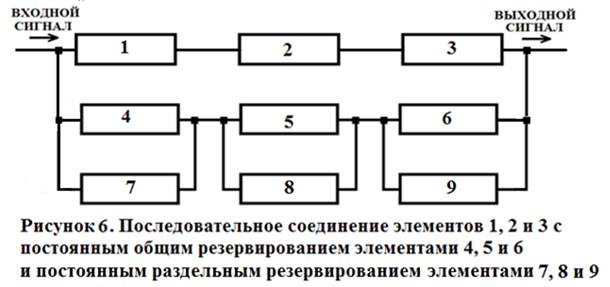
Для определения вероятности безотказной работы такой системы выполним ее разбиение на зоны, как показано на рисунке 7.

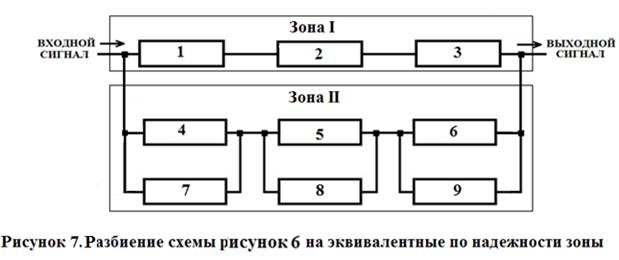
Зона I представляет собой последовательное по надежности соединение элементов 1, 2 и 3. Зона II представляет собой систему с раздельным постоянным резервированием элементов. Соответственно вероятности безотказной работы зон I зоны II определятся как:

Р_I(t) = { Р (t) }³ = 0,997³ = 0,991027.

Р_II(t) = [1 – {1 - (Р₄(t) }{1 - (Р₇(t) }] = [1 – {1 - (Р₅(t) }{1 - (Р₈(t) }] = [1 – {1 - (Р₆(t) }{1 - (Р₉(t) }] = (0,999991)³ = 0,999973.

С учетом разбиения на зоны, схема системы, представленной на рисунке 6, примет вид (рисунок 8):

Вероятность безотказной работы системы, представленной на рис 8. определится, как:

Р_с(t) = 1 – {1 - Р_I(t) } · {1 - Р_II(t) } = 1 – (1 - 0,991027)·(1 - 0,999973) = 1 – 0,008973·0,000027 = 0,999999758.

Данная система имеет надежность на порядок выше, чем абсолютно надежная система. Поэтому можно сделать вывод, что при помощи комбинированного резервирования можно получить существенное увеличение надежности системы. В этом случае система будет очень сложной и дорогостоящей.

ЗАКЛЮЧЕНИЕ

7. Выводы по материалу занятия.

8. Ответы на вопросы.

9. Задание на самостоятельную работу.

ЛИТЕРАТУРА

3. ГОСТ 27.002-89 Надежность в технике. Основные понятия. Термины и определения.

2. Надежность и диагностика систем электроснабжения железных дорог: Учебник для вузов ж/д транспорта/ А.В. Ефимов, А.Г. Галкин. – М.: УМК МПС России, 2000, с. 275 … 280.

«МОДЕЛИ ОТКАЗОВ ОБЪЕКТОВ СИСТЕМЫ ЭЛЕКТРОСНАБЖЕНИЯ ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА»

ВРЕМЯ – 2 часа

ЦЕЛИ ЗАНЯТИЯ:

1. Изучить модель отказа «нагрузка и прочность – случайные величины»

СОДЕРЖАНИЕ ЗАНЯТИЯ:

ВВОДНАЯ ЧАСТЬ – 5 мин.

УЧЕБНЫЕ ВОПРОСЫ:

1. МОДЕЛЬ ОТКАЗА «НАГРУЗКА И ПРОЧНОСТЬ – СЛУЧАЙНЫЕ ВЕЛИЧИНЫ» – 80 мин.

ЗАКЛЮЧЕНИЕ – 5 мин.

1. МОДЕЛЬ ОТКАЗА «НАГРУЗКА И ПРОЧНОСТЬ – СЛУЧАЙНЫЕ ВЕЛИЧИНЫ»

В большинстве случаев отказ какого-либо объекта системы электроснабжения железнодорожного транспорта происходит тогда, когда нагрузки, действующие на объект, превышают его прочность [1].

Нагрузки, действующие на объект, и прочность объект являются случайными величинами. Изменения этих величин, хотя и происходят случайно, но все равно подчиняются статистическим закономерностям. Поэтому рассматриваются не сами величины, а плотности вероятности их статистических распределений.

Обозначим плотность вероятности статистического распределения нагрузки на объект, как f_н(х), а плотность вероятности статистического распределения прочности объект, как f_п(х). В данном случае х – это некоторый характерный параметр, определяющий нагрузку на объект и его прочность исходя из физической сущности конкретного рассматриваемого процесса (сила тока, напряжение, давление, масса, сила и т.п.). В дальнейшем термин «плотность вероятности статистического распределения» заменим для простоты термином «плотность распределения».

С учетом принятых обозначений можно изобразить состояние объекта и нагрузку, действующую на него графически (рисунок 1).

На рисунке 1 графики функций f_н(х) и f_п(х) пересекаются и имеют некоторую общую область А. В этой области нагрузки на объект могут превышать его прочность. В этом случае вероятность отказа объект будет наибольшей.

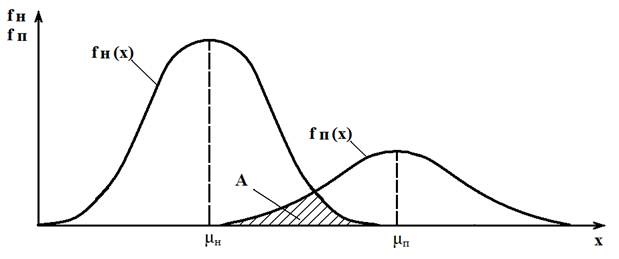
Рисунок 1. Графики плотности вероятности статистического распределения прочности объект f_п(х) и плотности распределения нагрузок на объект f_н(х): μ_н – математическое ожидание нагрузки; μ_п - математическое ожидание прочности.

Для выполнения расчетов и определения вероятности отказов объект следует определить условия, при которых под кривыми f_н(х) и f_п(х) возникнет общая область А. Для этого необходимо описать функции f_н(х) и f_п(х). Для этих целей на практике рассматривают 5 наиболее распространенных случаев:

1. Функции плотности распределения нагрузки f_н(х) и прочности f_п(х) имеют экспоненциальное распределение.

2. Функции плотности распределения нагрузки f_н(х) и прочности f_п(х) имеют нормальное распределение Гаусса.

3. Функции плотности распределения нагрузки f_н(х) и прочности f_п(х) имеют гамма- распределение.

4. Функция плотности распределения нагрузки f_н(х) имеет нормальное распределение Гаусса, а функция плотности распределения прочности f_п(х) имеет распределение Вейбулла.

5. Функции плотности распределения нагрузки f_н(х) и прочности f_п(х) имеют распределение Вейбулла.

Наиболее простым случаем является первый случай – когда функции плотности распределения нагрузки и прочности имеют экспоненциальное распределение. При этом вероятность отказа элемента определяется по формуле:

Q = 1 – λ_н/(λ_н + λ_п),

где λ_н и λ_п - параметры функций плотности распределений нагрузки и прочности.

Наиболее общим и распространенным является второй случай – когда функции плотности распределения нагрузки и прочности имеют нормальное распределение Гаусса (рисунок 1). Как видно из графиков рисунка, надежность элемента определяется взаимным расположением кривых f_н(х) и f_п(х), а также величинами математического ожидания нагрузки μ_н и математического ожидания прочности μ_п.

Отношение величины математического ожидания прочности μ_п к величине математического ожидания нагрузки μ_н называется коэффициентом запаса прочности К_З:

К_З= μ_п / μ_н.

Из рисунка 1 и выражения для определения К_З следует, что чем больше коэффициент запаса прочности. Тем меньше вероятность отказа элемента из-за того, что нагрузки на него превысят прочность. Увеличивая величину К_З мы сдвигаем функцию f_п(х) вправо. При определенном значении К_З ˃ К_КРЗ кривые f_н(х) и f_п(х) не будут пересекаться (рисунок 2). В данном случае К_КРЗ - это критическое значение коэффициента запаса прочности, обеспечивающее не пресечение кривых f_н(х) и f_п(х).

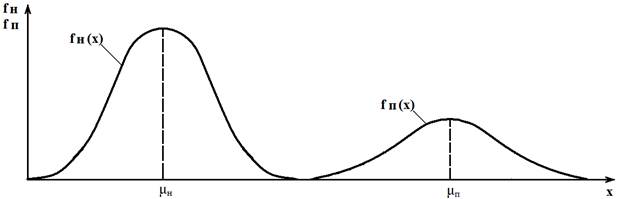
Рисунок 2. Расположение кривых f_н(х) и f_п(х) при условии К_З ˃ К_КРЗ.

За критическое значение коэффициента запаса прочности Ккрз принимается величина, при которой кривые f_н(х) и f_п(х) не пересекаются, т.е. когда нагрузка теоретически не может превысить прочность. Это условие можно соблюсти на определенном интервале времени. По мере старения и износа объекта его прочность будет снижаться, а следовательно и кривая f_п(х) будет смещаться влево в сторону кривой f_н(х).

Увеличение прочности требует применения более дорогостоящих материалов и усложнения конструкции объекта. Объект становится дорогим и материалоемким. Его надежность и ресурс при этом возрастают пропорционально затратам. На практике величина коэффициента запаса прочности выбирается в пределах К_З = 1,6 … 1.8, как, например, для железобетонных опор. Редко величина К_З = 2. Однако для особо нагруженных объектов СЭЖТ коэффициенты запаса прочности выбираются достаточно большими: для стальных тросов компенсаторов натяжения К_З = 4; для стальных продольных несущих тросов, фиксирующих и биметаллических поперечных тросов Кз = 3; для контактных проводов К_З = 2,5.

Речь идет о периоде нормальной эксплуатации объекта. Со временем коэффициент запаса прочности снижается.

Надежность объекта может быть повышена и без увеличения коэффициента запаса прочности К_З. Это достигается улучшением качества изготовления объекта, его конструктивным совершенством, а также путем улучшения системы эксплуатации. В результате этих и других мероприятий уменьшаются коэффициенты вариации плотности распределения нагрузки ν_н и вариации плотности распределения прочности ν_п. Коэффициенты вариации плотности распределения нагрузки и прочности определяются из соотношений:

ν_н = ϭ_н / μ_н; ν_п = ϭ_п / μ_п,

где ϭ_н и ϭ_п - соответственно величины рассеяния величин плотности распределения нагрузки и прочности (рисунок 3).

Рисунок 3. Расположение кривых f_н(х) и f_н1(х) относительно кривой f_п(х):

f_н(х) – плотность распределения нагрузки при обычном рассеянии ϭ_н; и f_н1(х) – плотность распределения нагрузки при уменьшенном рассеянии ϭ_{н1 .}

Уменьшая параметр рассеяния плотности распределения нагрузки при тех же максимальных ее значениях, добиваются того, что область А₁ пересечения кривых f_н1(х) и f_п(х) будет значительно меньше области А в случае пересечения кривых f_н(х) и f_п(х). В результате вероятность отказа объекта из-за превышения нагрузки над прочностью существенно снижается.

Пример 1. На двух сходных анкерных участках установлен контактный провод МФ-100. Сила натяжения проводов у компенсаторов составляет 10 кН, что обеспечено установкой 10 грузов массой по 25 кг каждый. Коэффициент передачи компенсатора составляет 4:1. Провода выдерживали нагрузку от прохождения ПС массой 6 тыс. тонн при нормированном ветре и гололеде. Прошло время и провода подверглись износу. Их сечение уменьшилось. На одном анкерном участке провод эксплуатировался правильно и при достижении его износа 10 мм² был снят один груз компенсатора. Натяжение уменьшилось до 9 кН. Провод продолжал выдерживать проход ПС массой 6 тыс. тонн при ветре и гололеде.

На другом участке измерение и учет износа велись менее тщательно. При достижении износа 10 мм² груз компенсатора своевременно снят не был. При проходе ПС массой 6 тыс. тонн в условиях ветра и гололеда провод не выдержал нагрузки и оборвался.

Пример показывает важность соблюдения правил технической эксплуатации КС, что ведет к уменьшению вариации нагрузок, а следовательно и к повышению надежности.

Применение современных технологий позволяет уменьшить погрешности при изготовлении элементов СЭЖТ. Коэффициент вариации плотности распределения прочности уменьшается. В этом случае говорят, что увеличивается равнопрочность объекта. На рис. 4 представлен случай повышения надежности объекта за счет одновременного снижения коэффициента вариации плотности распределения нагрузки ν_н и коэффициента вариации плотности распределения прочности ν_п.

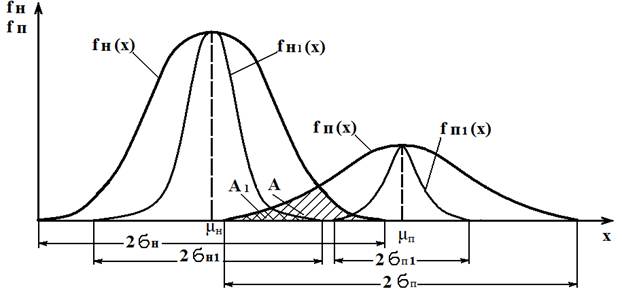
Рисунок 4. Расположение кривых f_н(х) и f_н1(х) относительно кривой f_п(х) и кривой f_п1(х) - при реализации кривых f_н1(х) и f_п1(х) область их пересечения отсутствует.

На рисунке 4 показано, что при тех же значениях математического ожидания прочности μ_п и нагрузки μ_н, а следовательно при том же коэффициенте запаса прочности К_З за счет уменьшения коэффициентов вариации плотности распределения нагрузки ν_н и прочности ν_п удается исключить пересечение кривых f_н1(х) и f_п1(х). В результате надежность объекта существенно возрастает, т.к. на определенном этапе его эксплуатации нагрузка не может превысить прочность. Таков практический результат повышения дисциплины эксплуатации объекта и качества его изготовления.

Пример 2. На тяговой подстанции применяются изоляторы с математическиможиданием электрической прочности μ_п = 30 кВ и параметром рассеивания электрической прочности ϭ_п = 2,7 кВ.

При коммутационных перенапряжениях возникают нагрузки с математическим ожиданием μ_н = 20 кВ и рассеиванием ϭ_п = 5 кВ.

Определить коэффициент запаса электрической прочности изоляторов и коэффициенты вариации прочности и нагрузки. Оценить возможность отказа изоляторов из-за превышения нагрузки над прочностью.

Решение:

1. Определяем коэффициент запаса электрической прочности изоляторов:

К_З = μ_п / μ_н = 30 кВ / 20 кВ = 1,5.

2. Определяем коэффициенты вариации:

ν_п = ϭ_п / μ_п = 2,7 кВ / 30 кВ = 0,09; ν_н = ϭ_н / μ_н = 5 кВ / 20 кВ = 0,25.

3.Определяем возможность отказа изоляторов из-за превышения нагрузки над прочностью:

Максимальная нагрузка на изолятор х_{н мах} может составить:

х_{н мах} = μ_н + ϭ_н = 20 кВ + 5 кВ = 25 кВ.

Минимальная электрическая прочность изолятора может составить:

х_{п мin} = μ_п – ϭ_п = 30 кВ – 2,7 кВ = 27,3 кВ.

Поскольку х_{п мin} ˃ х_{н мах}, то кривые f_н(х) и f_п(х) не пересекаются. Это означает, что на этапе нормальной эксплуатации электрическая прочность изоляторов всегда больше электрической нагрузки на них. При этом не может быть их пробоя.

В эксплуатации происходит загрязнение изоляторов и их старение. В результате коэффициент вариации плотности распределения прочности возрастает. При ν_п ˃ 0,167 ϭ_п ˃ 5 кВ. В этом случае, при тех же электрических нагрузках х_{п мin} ˂ х_{н мах}, кривые f_н(х) и f_п(х)) пересекаются и пробой изоляторов возможен.

Со временем эксплуатации ухудшается не только электрическая прочность изоляторов. Ухудшаются свойства трансформаторного оборудования и из-за износа коммутационного оборудования возрастают перенапряжения. Все это ведет к увеличению коэффициента вариации плотности распределения нагрузки ν_н. Это также ведет к снижению надежности работы изоляторов и к повышению вероятности их отказа.

Рассмотренная нами модель отказа «Нагрузка и прочность – случайные величины» имеет широкое распространение на практике и объясняет снижение эксплуатационной надежности объектов СЭЖТ. Надежность может быть восстановлена путем совершенствования системы эксплуатации и повышения качества изготовления отдельных изделий и системы в целом.

ЗАКЛЮЧЕНИЕ

4. Выводы по материалу занятия.

5. Ответы на вопросы.

6. Задание на самостоятельную работу.

ЛИТЕРАТУРА

4. Надежность и диагностика систем электроснабжения железных дорог: Учебник для вузов ж/д транспорта/ А.В. Ефимов, А.Г. Галкин. – М.: УМК МПС России, 2000.

Дата добавления: 2014-01-05