
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
И при соединении звездой и треугольником
|
|
|
|
Соотношения активных мощностей при симметричной нагрузке
Лекция 7
Активная мощность трёхфазной цепи, в которой нагрузка соединена звездой, определяется через фазные значения напряжения и тока:
 . (3.24)
. (3.24)
Для активной нагрузки угол сдвига фаз между напряжением и током 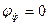 , тогда
, тогда 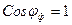 . Так как фазное и линейное напряжения соответствуют выражению
. Так как фазное и линейное напряжения соответствуют выражению
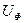 =
= 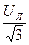 , (3.25)
, (3.25)
а фазный ток является линейным, то по закону Ома определим его значение
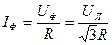 , (3.26)
, (3.26)
где  - фазное сопротивление нагрузки.
- фазное сопротивление нагрузки.
Подставив в формулу (3.24) выражения (3.25) и (3.26), определим активную мощность трёхфазной цепи, соединённой звездой:
 ∙
∙ ∙
∙ =
= 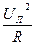 . (3.27)
. (3.27)
Активную мощность трёхфазной цепи, в которой нагрузка соединена треугольником, также можно определить по формуле (3.24). При этом фазное напряжение 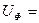
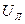 , а фазный ток
, а фазный ток  , поэтому активную мощность трёхфазной цепи, соединённой треугольником, можно определить по формуле:
, поэтому активную мощность трёхфазной цепи, соединённой треугольником, можно определить по формуле:

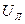 ∙
∙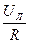 =
= . (3.28)
. (3.28)
Используя формулы (3.27) и (3.28), определим коэффициент отношений активных мощностей звезды и треугольника, а также коэффициент их обратных отношений:
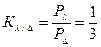 ;
;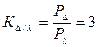 . (3.29)
. (3.29)
3.8. Вращающееся магнитное поле трёхфазной системы переменного тока
Действие трёхфазной машины основано на использовании вращающегося магнитного поля.
На рис.3.27 показана трёхфазная обмотка машины переменного тока в виде трёх статорных обмоток, сдвинутых на угол 120  , состоящих из одного витка. Обмотки соединены звездой. Пусть в витках обозначения А, В, С являются началами обмоток; X, Y, Z - концами обмоток.
, состоящих из одного витка. Обмотки соединены звездой. Пусть в витках обозначения А, В, С являются началами обмоток; X, Y, Z - концами обмоток.

Рис.3.27. Модель трёх статорных обмоток трёхфазной машины, состоящих из одного витка и соединенных звездой
При подаче трёхфазного питания на фазы А, В, С (режим электродвигателя), по обмоткам статора пройдут мгновенные токи:  ,
, 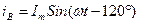 ,
, 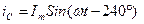
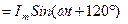 , фазы которых смещены на угол 120
, фазы которых смещены на угол 120 . Допустим, что токи в точках А, В, С является положительными и направлены на зрителя, а токи в точках X, Y, Z является отрицательными и направлены от зрителя.
. Допустим, что токи в точках А, В, С является положительными и направлены на зрителя, а токи в точках X, Y, Z является отрицательными и направлены от зрителя.
На рис.3.28 изображена временная зависимость фаз мгновенных токов, имеющих одинаковые амплитуды и частоту.
Токи возбуждают переменные магнитные поля. Направления магнитных полей катушек показаны на рис.3.27 векторами фаз магнитных индукций:
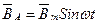 ;
;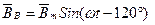 ;
;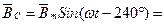
 ,
,
расположенных под углом 90 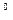 к плоскостям катушек и относительно друг друга под углом 120
к плоскостям катушек и относительно друг друга под углом 120 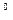 . Определим векторы результирующих магнитных индукций
. Определим векторы результирующих магнитных индукций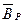 для моментов времени t
для моментов времени t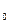 , t
, t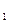 , t
, t , указанных на рис.3.28.
, указанных на рис.3.28.

Рис.3.28. Временная зависимость фаз мгновенных токов трёхфазной машины
Для этих моментов рассмотрим схематические изображения рис.3.29 фаз обмоток статора, по которым проходят токи с направлениями, соответствующими рис.3.28.
Направления магнитных полей Ф, для рассматриваемых моментов, определяются по правилу буравчика, аналогично направлены векторы результирующих магнитных индукций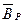 . Из рисунка видно, что происходит вращение магнитного поля трёхфазной системы по часовой стрелке.
. Из рисунка видно, что происходит вращение магнитного поля трёхфазной системы по часовой стрелке.
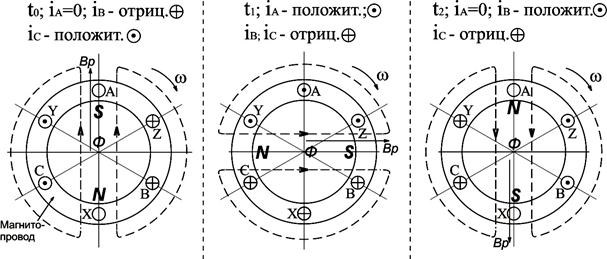
Рис.3.29. Схемы, поясняющие вращение магнитного поля трёхфазной системы
Выполним расчёт векторов результирующей магнитной индукции для моментов времени t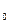 ,t
,t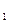 , t
, t .
.
Для t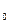 ,
, 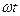 = 0
= 0 :
:
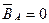 ;
;
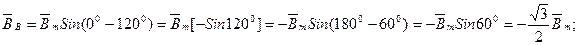
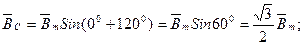
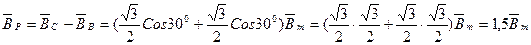 .
.
Для t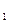 ,
, 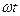 = 90
= 90 : Для t
: Для t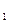 ,
, 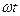 = 90
= 90 :
:
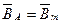 ;
; 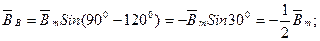
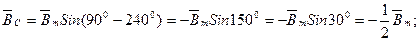
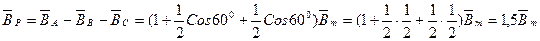 .
.
Для t ,
, 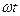 = 180
= 180 : Для t
: Для t ,
, 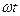 =180
=180 :
:
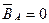 ;
; 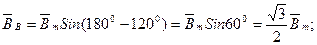
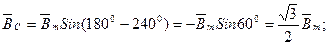
 .
.
По данному расчёту на рис.3.30 построена векторная диаграмма положений векторов результирующей магнитной индукции.
Таким образом, во времени происходит равномерное непрерывное изменение направления магнитного поля, созданного трёхфазной обмоткой, при этом магнитное поле вращается с постоянной скоростью. Если изменить чередование фаз, изменив подключение к сети любых двух из трёх обмоток, то изменится направление вращения магнитного поля. В момент t результирующий магнитный поток направлен по вертикальной оси. Через один период магнитный поток и магнитная индукция повернутся на один полный оборот и будут такими же, как при t = 0. Если частота тока f, то магнитное поле совершит f оборотов в секунду, тогда частота вращения магнитного поля в минуту n = 60 ∙f/p, где р - число пар полюсов или число катушек на фазу. Для трёх катушек на фазу p=1, n=60 ∙f. Для шести катушек на фазу n =
результирующий магнитный поток направлен по вертикальной оси. Через один период магнитный поток и магнитная индукция повернутся на один полный оборот и будут такими же, как при t = 0. Если частота тока f, то магнитное поле совершит f оборотов в секунду, тогда частота вращения магнитного поля в минуту n = 60 ∙f/p, где р - число пар полюсов или число катушек на фазу. Для трёх катушек на фазу p=1, n=60 ∙f. Для шести катушек на фазу n =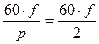 , так как 2р=4, р=2.
, так как 2р=4, р=2.
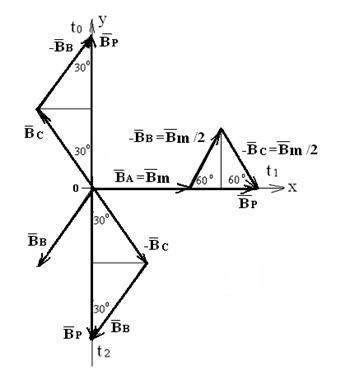
Рис.3.30. Векторная диаграмма положений векторов результирующей магнитной индукции для моментов времени t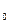 ,t
,t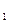 , t
, t .
.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 630; Нарушение авторских прав?; Мы поможем в написании вашей работы!