План лекции. Случайные процессы и их классификация

Случайные процессы и их классификация

Случайным процессом называется случайная функция аргумента t, где t текущее время. Случайный процесс обозначается прописными буквами греческого алфавита , , 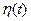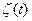. Допустимо и другое обозначение, если оно заранее оговорено.

Когда говорят о как о случайной функции, то имеют в виду, что для выбранного аргумента t вид функции до получения опытных данных не определен. Конкретный вид случайного процесса, который наблюдается во время опыта, например на осциллографе, называется реализацией этого случайного процесса.

Реализации x(t), y(t), z(t) по отношению к соответствующим процессам , , 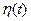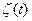играют ту же роль, что и возможные значения х, у, z по отношению к своим случайным величинам 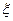, , 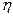. Вид конкретной реализации x(t) может задаваться определенной функциональной зависимостью аргумента t или графиком. Другими словами, это обычная детерминированная функция аргумента t.

В зависимости от того, непрерывные или дискретные значения принимают аргумент t и реализация х, различают пять основных видов случайных процессов. Поясним эти виды с указанием примеров.

Непрерывный случайный процесс характеризуется тем, что t и х являются непрерывными величинами (рис. 1,а). Таким процессом, например, является шум на выходе радиоприемного устройства.

Дискретный случайный процесс характеризуется тем, что t является непрерывной величиной, а х - дискретной (рис. 1,б). Переход от 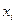к 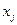происходит в любой момент времени. Примером такого процесса является процесс, характеризующий состояние системы массового обслуживания, когда система скачком в произвольные моменты времени t переходит из одного состояния в другое. Другой пример это результат квантования непрерывного процесса только по уровню.

Случайная последовательность характеризуется тем, что t является дискретной, а х — непрерывной величинами (рис. 1,в). В качестве примера можно указать на временные выборки в конкретные моменты времени из непрерывного процесса.

Дискретная случайная последовательность характеризуется тем, что t и х являются дискретными величинами (рис. 1,г). Такой процесс может быть получен в результате квантования по уровню и дискретизации по времени. Такими являются сигналы в цифровых системах связи.

Случайный поток представляет собой последовательность точек, дельта-функций или событий (рис. 1, д, ж) в случайные моменты времени. Этот процесс широко применяется в теории надёжности, когда поток неисправностей радиоэлектронной техники рассматривается как случайный процесс.

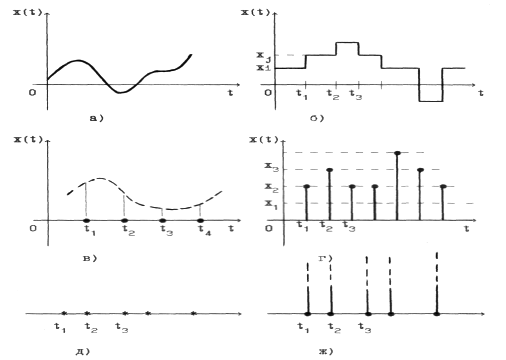
Рис. 1

В статистической радиотехнике все процессы также можно клас­сифицировать по виду их функциональной зависимости. Например, различают детерминированные, квазидетерминированные и случайные модулированные колебания.

у детерминированного процесса или колебания вид функциональной зависимости полностью определен. Например, гармоническое колебание с известными амплитудой, частотой и фазой.

Квазидетерминированный процесс характеризуется заданной фун­кциональной зависимостью во времени, которая, однако, зависит также от параметров, являющихся случайными величинами. Например, гармоническое колебание со случайной амплитудой или фазой. В этом случае из-за случайности своих параметров процесс имеет множество реализаций, одна из которых, но какая именно - неизвестно, проявится в испытании, так что квазидетерминированный процесс является случайным.

К случайным модулированным колебаниям относятся модулированные колебания, у которых тот или иной параметр модулируется случайным образом, то есть у которого модулирующая функция является случайным процессом. Таким образом, модулированное колебание, являясь функцией случайного процесса, также представляет собой случайный процесс. Примерами являются AM, ЧМ и ФМ колебания, у которых амплитуда, частота или фаза изменяются в соответствии со случайной модулирующей функцией.

Контрольные вопросы:

1. Что называется случайным процессом?

2. Назовите области статистического моделирования?

3. Назовите этапы моделирования случайных величин?

Тема № 1 «Общие сведения о случайных процессах»

Лекция № 2 «Способы описания случайных процессов»

Цель лекции.

а) учебная цель:

Целью является формирование у слушателей целостного представления о принципах применения элементов теории вероятностей при моделировании сетевых процессов – элемента систем массового обслуживания.

1. Способы описания случайных процессов

2. Эргодическое свойство стационарных процессов

Дата добавления: 2014-01-05