Эргодическое свойство стационарных процессов

Среди всех стационарных процессов имеется часть, которая обладает эргодическим свойством. Поясним это свойство.

Пусть имеется одна длинная реализация x(t) случайного процесса 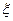(t). Эта реализация определена на интервале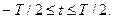

Найдем среднее значение этой реализации путем ее усреднения во времени на достаточно большом интервале:

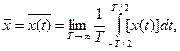(2.14)

где черта сверху означает усреднение по времени, среднее значение 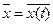является постоянной величиной, не зависящей от t.

Аналогично можно найти среднее значение квадрата флюктуации и среднее значение произведения флюктуации, смещенных одна относительно другой на интервал :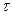

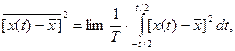(2.15)

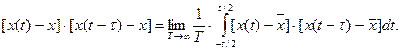(2.16)

По своему физическому смыслу величины (2.14), (2.15), (2.16) являются числовыми характеристиками, совпадающими со средним значением, дисперсией и корреляционной функцией процесса 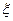(t). Однако они получены в результате усреднения во времени одной длинной реализации x(t) или функции от нее.

Говорят, что стационарный процесс обладает эргодическим свойством, если с вероятностью, близкой к единице, числовые характеристики, полученные в результате усреднения одной длинной реализации по времени, равны этим же характеристикам, полученным в результате усреднения по ансамблю. При этом усреднением по ансамблю называют определение числовых характеристик с использованием плотности вероятности, т.е. по формулам (2.11), (2.12) и (2.13), так как плотность вероятности характеризует всю совокупность или ансамбль реализаций.

Таким образом, для эргодического стационарного процесса справедливы равенства:

,

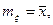
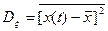(2.17)

Само слово "эргодический"происходит от греческого "эргон", что означает "работа". Эргодическое свойство является удобной рабочей гипотезой для расчета числовых характеристик стационарного процесса, когда располагают одной длинной его реализацией. Физически это обосновано тем, что одна длинная реализация может содержать сведения обо всех реализациях этого случайного процесса.

Контрольные вопросы:

1. Назовите способы представления случайных процессов?

2. Какой случайный процесс называется стационарным?

3. Какой случайный процесс называется нестационарным?

4. Какой случайный процесс называется эргодическим?

Тема № 2 «Сетевое моделирование процессов»

Лекция № 3 «Назначение сетевого моделирования»

Цель лекции.

а) учебная цель:

Целью является формирование у слушателей целостного представления о принципах применения элементов теории вероятностей при моделировании сетевых процессов – элемента систем массового обслуживания.

Дата добавления: 2014-01-05