
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Колебательные звенья. Особые звенья: неминимально-фазовые устойчивые звенья, неустойчивые звенья
|
|
|
|
Колебательное звено описывается уравнением второго порядка
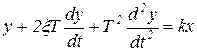 (1.7.48)
(1.7.48)
при степени затухания 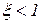 , что соответствует комплексным корням характеристического уравнения
, что соответствует комплексным корням характеристического уравнения

Постоянная времени Т колебательного звена связана с его резонансной частотой ω0 соотношением
 (1.7.49)
(1.7.49)
и в 2π раз меньше периода резонансных колебаний
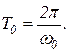 (1.7.50)
(1.7.50)
Примерами колебательного звена могут служить упругая механическая система с существенным влиянием массы, электрический колебательный контур (рисунок 1.7.14).

Рисунок 1.7.14 – Примеры колебательного звена
Комплексный коэффициент усиления колебательного звена
 (1.7.51)
(1.7.51)
Вводя безразмерную частоту  можно
можно  выразить следующим образом:
выразить следующим образом:
 (1.7.52)
(1.7.52)
На рисунке 1.7.15, а, б, в показаны частотные характеристики колебательного звена. Как видно из рисунка 1.7.15, а, годограф частотной характеристики проходит через два квадранта IV и III и пересекает мнимую ось при  . При этом
. При этом

С уменьшением ξ петля, охватываемая годографом, увеличивается (см. пунктир), и при 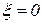 характеристика вырождается в две полупрямые: I — от
характеристика вырождается в две полупрямые: I — от  до
до 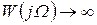 при
при 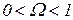 и II ― от
и II ― от  до
до 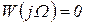 при
при  . Инверсная характеристика
. Инверсная характеристика  проходит через два квадранта I и II и уходит в бесконечность параллельно вещественной оси при
проходит через два квадранта I и II и уходит в бесконечность параллельно вещественной оси при 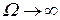 .
.
Амплитудно-частотная и фазочастотная характеристики выражаются уравнениями:
 (1.7.53)
(1.7.53)
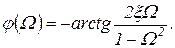 (1.7.54)
(1.7.54)
При  эти характеристики соответственно проходит через точки
эти характеристики соответственно проходит через точки  и
и 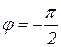 . При
. При  кривая
кривая  имеет максимум
имеет максимум
 (1.7.55)
(1.7.55)
при
 (1.7.56)
(1.7.56)
Передаточная функция колебательного звена
 (1.7.57)
(1.7.57)
Корнями характеристического уравнения  будут
будут

где  — коэффициент затухания;
— коэффициент затухания;
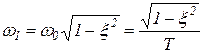 ― собственная частота колебаний звена.
― собственная частота колебаний звена.
Переходная функция
 (1.7.58)
(1.7.58)
Весовая функция
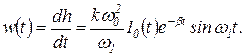 (1.7.59)
(1.7.59)
Графики переходной и весовой функций колебательного звена показаны на рисунке 1.7.15, г и д.

Рисунок 1.7.15 – Характеристики колебательного звена
Кроме рассмотренных типовых линейных звеньев, в системах автоматического управления встречаются звенья, которые по характеристикам существенно отличаются от типовых. К числу таковых относятся: неминимально-фазовые звенья, передаточные функции которых дробно-рациональны и имеют нули в правой полуплоскости: неустойчивые звенья, имеющие полюса в правой полуплоскости; звенья с распределёнными параметрами, которые могут быть разделены на иррациональные звенья, описываемые иррациональными передаточными функциями, и трансцендентные, описываемые трансцендентными передаточными функциями. В звеньях с распределенными параметрами количество особенностей передаточных функций может стремиться к бесконечности и анализ динамических свойств системы требует рассмотрения вспомогательных вопросов. Это связано с тем, что звено описывается уже не обыкновенными линейными дифференциальными уравнениями, а уравнениями в частных производных.
Рассмотрим звенья каждой из всех перечисленных групп и примеры реальных элементов, соответствующих им.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 1672; Нарушение авторских прав?; Мы поможем в написании вашей работы!