
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Погрешности измерительных устройств
|
|
|
|
Инструментальная <…> погрешность (или погрешность измерительных устройств) имеет определяющее значение для наиболее распространенных технических измерений.
На рис. 1.6 приведена классификация погрешностей измерительных устройств по ряду признаков.
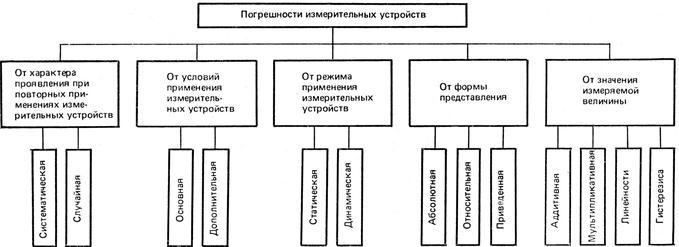
Рис. 1.6. Классификация погрешностей измерительных устройств
По характеру проявления при повторных измерениях одного и того же значения физической величины принято выделять систематическую и случайную погрешности (или составляющие погрешности) измерительных устройств. В эти понятия в основном вкладывается тот же смысл, что и в понятия систематической и случайной погрешности измерений <…>. Особенность здесь состоит в том, что всякое измерительное устройство предназначается для внесения определенности в исследуемый процесс, а наличие случайной составляющей погрешности приводит к неоднозначности. В связи с этим первая задача, которая обычно решается при создании измерительных устройств, состоит в том, чтобы случайную погрешность сделать незначительной. Если это условие выполняется, а элементы, входящие в состав измерительного устройства, стабильны, можно путем градуировки <…> обеспечить достаточно малые систематические погрешности измерительного устройства. Рассмотренная концепция используется как основная при создании рабочих средств измерений и, в частности, измерительных устройств для технологических измерений.
В зависимости от условий применения измерительных устройств различают основную и дополнительную погрешности (см. рис. 1.6).
Основной погрешностью средства измерений называют погрешность при использовании его в нормальных условиях. Нормальными условиями применения средств измерений называют условия, при которых влияющие величины имеют номинальные значения или находятся в пределах нормальной области значений. Нормальные условия применения указываются в стандартах или технических условиях на средства измерений. При использовании средств измерений в нормальных условиях считают, что влияющие на них величины практически никак не изменяют их характеристики.
Дополнительной погрешностью измерительного преобразователя (или изменением показаний измерительного прибора) называют изменение его погрешности, вызванной отклонением одной из влияющих величин от ее нормативного значения или выходом ее за пределы нормальной области значений. Дополнительная погрешность может быть вызвана изменением сразу нескольких влияющих величин.
Изменение погрешности, как и других характеристик и параметров измерительных устройств под действием влияющих величин, описывается функциями влияния <…>.
Иными словами, дополнительная погрешность – это часть погрешности, которая добавляется (имеется в виду алгебраическое сложение) к основной в случаях, когда измерительное устройство применяется в рабочих условиях. Рабочие условия обычно таковы, что изменения значений влияющих величин на них существенно больше, чем для нормальных условий, т. д. область рабочих (часть этой области называют расширенной областью) условий включает в себя область нормальных условий.
В некоторых случаях основная погрешность измерительных устройств определяется для рабочей области изменения значений влияющих величин. В этих случаях понятие дополнительной погрешности теряет смысл.
В зависимости от режима применения различают статическую и динамическую погрешности измерительных устройств <…>.
По форме представления принято различать абсолютную, относительную и приведенную погрешности измерительных устройств (рис. 1.6). Для измерительных приборов и преобразователей определение этих погрешностей специфично. У измерительных приборов имеется шкала, отградуированная в единицах входной величины, либо шкала, отградуированная в условных единицах с известным множителем шкалы, поэтому результат измерения представляется в единицах входной величины. Это обусловливает простоту определения погрешности измерительных приборов.
Абсолютной погрешностью измерительного прибора Δ называют разность показаний прибора Х п и истинного (действительного) Х д значения измеряемой величины:
| Δ= X п– X д. | (1.11) |
Действительное значение определяется с помощью образцового прибора или воспроизводится мерой.
Относительной погрешностью измерительного прибора называют отношение абсолютной погрешности измерительного прибора к действительному значению измеряемой величины. Относительную погрешность выражают в процентах:
| δ=Δ100/ X д. | (1.12) |
Так как Δ<< X д или Х п то в выражении (1.12) вместо значения Х д может быть использовано значение Х п.
Приведенной погрешностью измерительного прибора называют отношение абсолютной погрешности измерительного прибора к нормирующему значению ХN. Приведенную погрешность также выражают в процентах:
| γ=Δ100/ XN. | (1.13) |
В качестве нормирующего значения используется верхний предел измерений, диапазон измерений и др., т. е.
| γ=Δ100/(X в– X н). | (1.14) |


Рис. 1.7. Реальные функции преобразования измерительных устройств
Аддитивной (получаемой путем сложения), или погрешностью нуля измерительных устройств, называют погрешность, которая остается постоянной при всех значениях измеряемой величины.
На рис. 1.7, а показано, что реальная функция преобразования Y = ƒ р(X) несколько смещена относительно номинальной Y = ƒ н(X) т. е. выходной сигнал измерительного устройства при всех значениях измеряемой величины X будет больше (или меньше) на одну и ту же величину, чем он должен быть, в соответствии с номинальной функцией преобразования.
Мультипликативной (получаемой путем умножения), или погрешностью чувствительности измерительных устройств, называют погрешность, которая линейно возрастает (или убывает) с увеличением измеряемой величины.
Графически появление мультипликативной погрешности интерпретируется поворотом реальной функции преобразования относительно номинальной (рис. 1.7, в).
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 1246; Нарушение авторских прав?; Мы поможем в написании вашей работы!