Лекция №5. Прямоугольный металлический волновод

.

По закону Снелля,

,

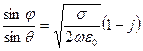откуда видно, что в хорошо проводящей среде преломленная волна распространяется под комплексным углом и поэтому является неоднородной плоской волной (см. рисунок 4.1а).

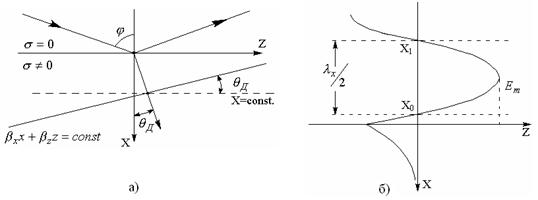
Рисунок 4.1 – Падение плоской электромагнитной волны на границу раздела сред между воздухом и металлом: а) образование неоднородной плоской волны; б) образование стоячей волны

У неоднородной плоской волны поверхности равной амплитуды и поверхности равной фазы не совпадают. Поверхность равной амплитуды перпендикулярна оси х, т.е. на рисунке 4.1,а показана как х=const. Поверхности равной фазы соответствует плоскость .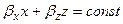

Во второй среде направление распространения волны образует угол q_Д с осью x. q_Д - истинный (действительный) угол:

.

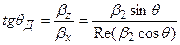Волна расположена перпендикулярно поверхностям равных фаз.

Учитывая, что для металлов:

,

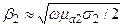тогда 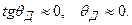То есть при любом угле падения j на поверхность хорошо проводящей среды преломлённая волна распространяется практически вдоль нормали к границе раздела.

Плоскости равных фаз и амплитуд практически совпадают – волна однородная. Волна – поперечная, причём Е и Н сдвинуты по фазе на .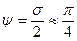

Так как амплитуда быстро убывает по экспоненте из-за большого затухания (см. рисунок 4.1,б), то поле есть практически в тонком поверхностном слое (явление поверхностного эффекта), причём во второй среде есть продольная составляющая.

По закону Ома: J = dE, весь ток сосредоточен возле поверхности. Эффективное сечение меньше геометрического, а активное сопротивление на ВЧ может быть во много раз больше, чем по постоянному току (проводник можно выполнить в виде трубы), т.е. полагают, что ток течёт в виде бесконечно тонкого слоя.

,

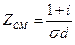где Z_СМ – поверхностное сопротивление проводника, d – глубина проникновения.

В первой среде ЭМП имеет структуру плоской волны, распространяющейся вдоль поверхности раздела (вдоль z) – направленная волна. Поверхности равных фаз – плоскости, перпендикулярные z. Амплитуды E и H зависят от x и от j. Поверхности равных амплитуд – плоскости, перпендикулярные x (см. рисунок 4.1,б).

Эта волна – неоднородная плоская волна, у которой есть продольная составляющая H_z (для волны с параллельной поляризацией – E_z).

Фазовая скорость:

,

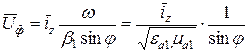то есть 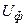больше 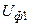, но меньше 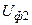. Причём, чем больше j, тем меньше 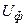. Длина волны вдоль z:

.

Изменение Е и Н вдоль оси x имеет характер стоячей волны в первой среде (см. рисунок б):

.

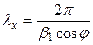Поперечные составляющие изменяются в фазе, а продольная сдвинута на 90°, в результате комплексный вектор Пойнтинга.

В среднем энергия распространяется только вдоль оси z, а в перпендикулярном по отношению к z направлении – только реактивный поток энергии. Это дает возможность создать направленную передачу ЭМВ, т.е. линии передач и другие устройства сверхвысоких частот (УСВЧ).

Классифицировать УСВЧ будем по функциям (см. таблица 4.1), которые они выполняют в линии передачи, независимо от того, для какой цели выполняется та или иная функция.

Линии передачи принято классифицировать по типу направляемых волн.

Типы волн:

1) поперечные или волны Т-типа – отсутствуют составляющие E и Н, направленные вдоль направления распространения энергии (T-transfers (поперечные)) Т-(ТЕМ);

2) электрические (Е- типа) Е-(ТМ);

3) магнитные (Н-типа) Н-(ТЕ);

4) смешанные (HE- типа) или гибридные.

Кроме того, все линии передачи делят на два больших класса:

1) закрытого типа – вся энергия сосредоточенна в пространстве, ограниченном металлической оболочкой от внешней среды;

2) открытого типа - поле, строго говоря, распределено во всем пространстве (подавляющая часть вблизи), поэтому параметры этих линий подвержены влиянию окружающей среды (метеоусловия, расположенные вблизи объекты и т.д.)

Т а б л и ц а 4.1 – Классификация устройств СВЧ

Наименование класса устройств	Функциональные признаки
1. Отрезки регулярных линий передач	Направленная передача ЭМЭ
2. Соединительные устройства	Соединения отрезков регулярных линий, элементов или узлов
а) Неподвижные и подвижные сочленения
б) Уголки и изгибы
в) Трансформаторы и фильтры типов волн
г) Вращающиеся сочленения
3. Делители мощности	Разделение энергии, передаваемой в одном канале, на несколько каналов или сложение энергии из нескольких каналов в одном
4. Переключающие устройства (коммутаторы)	Временные соединения различных каналов
5. Развязывающие устройства	Понижение уровня мощности, проходящей из одного канала в другой, или полная развязка между каналами
а) Аттенюаторы
б) Направленные ответвители
в) Циркуляторы
г) Вентили
6.Поляризационные преобразователи	Преобразование поляризации проходящих волн
7. Фазирующие устройства	Поддержание или изменение фазы или разности фаз колебаний в линии
а) Фазовращатели
б) Секции дифференциального Фазового сдвига
8. Мостовые (гибридные) соединения	Сложение, вычитание и калиброванное разделение мощности ЭМВ в четырех канальном соединении
а) Двойные Т-образные
б) Щелевые
в) Кольцевые
г) Шлейфовые
9. Защитные устройства	Предохранение нагрузки или узла от чрезмерной мощности
10. Согласующие устройства	Согласование тракта в целом его отдельных элементов и узлов для получения заданного коэффициента отражения
11. Симметрирующие устройства	Переход от несимметричной линии или узла к симметричной линии или узлу.

Так как линии передачи состоят из линейных сред то для упрощения их анализа удобно представить поперечные проекции поля 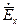,,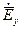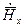и 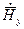через продольные проекции поля 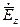и .

Введем два параметра:

1) продольное волновое число .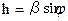

2) поперечное волновое число 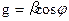т.е. .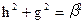

Особенность направляемых волн: комплексная амплитуда каждой из шести проекций векторов Е и Н зависит от пространственных координат по закону:

.

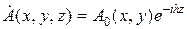Начальную фазу волны всегда можно подобрать так, чтобы 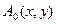- была действительной. Сторонние источники отсутствуют, и поле описывается уравнениями Максвелла. Путем несложных преобразований получаем связь между продольными и поперечными составляющими поля:

;

;

;

.

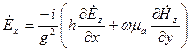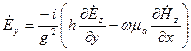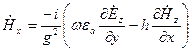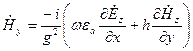Аналогично в любой другой системе координат.

Итак, достаточно найти лишь две функции для любой направляющей системы, а остальные проекции определяют через них .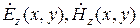

Прямоугольный металлический волновод – это полая металлическая идеально проводящая (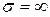) труба с поперечным сечением прямоугольной формы (см. рисунок 5.1).

Рисунок 5.1 – Прямоугольный металлический волновод

Полагаем, что волновод заполнен средой с параметрами (воздух) 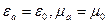. Внутри волновода на всем протяжении оси могут существовать волны типа – H:

Для этих волн характерно .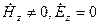

Функция 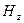является решением уравнения Гельмгольца:

,

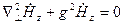где 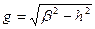– поперечное волновое число.

При решении уравнения Гельмгольца следует учитывать граничные условия (тангенциальная составляющая Е на металле обращается в 0):

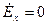при y = 0, y = b;

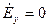при x = 0, x = а.

Решая уравнение Гельмгольца, получаем:

.

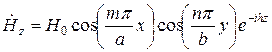Решения отличные от нуля возможны только при условии:

,

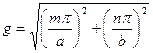где m и n – любые целые положительные числа не равные нулю одновременно (иначе силовые линии магнитного поля Н - незамкнуты и нарушается четвертое уравнение Максвелла).

Каждому значению g, (собственное значение) соответствует одно из множества решений уравнений Максвелла, которое в данном случае называют волной 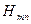, где m и n – индексы волны данного типа. Физически они означают количества стоячих полуволн, возникающих внутри волновода вдоль координатных осей x и y соответственно.

Используя формулы перехода (), получаем выражения для остальных проекций 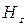. В результате структура ЭМП волны типа 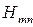описывается формулами:

;

; .

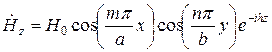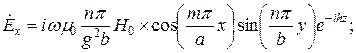
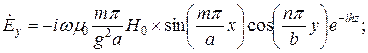
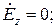
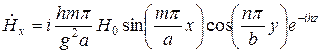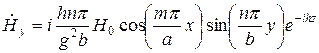Приведенная система формул содержит исчерпывающую информацию об электромагнитном поле волн типа 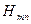. Картина поля периодична вдоль оси z; пространственным периодом служит длина волны в волноводе:

. (5.1)

Продольное волновое число 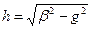определяет рабочую область волновода. Если рабочая длина волны 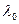мала настолько, что 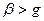, то h-действительна, и электромагнитное колебание распространяется в виде бегущей волны постоянной амплитуды. Если увеличить 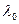так, что , то вместо бегущих волн в волноводе могут существовать лишь не распространяющиеся колебания, амплитуда которых уменьшается по экспоненте вдоль z, а фаза во всех поперечных сечениях постоянна – волновод работает в режиме отсечки. Пограничный случай возникает на такой рабочей частоте, когда: .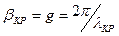

При этом h = 0, 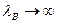, а длину волны генератора называют критической:

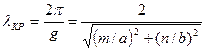. (5.2)

Используя выражения (5.1) можно получить зависимости 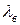от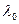

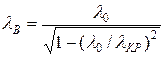, (5.3)

которая называется дисперсионной характеристикой волновода. Эта характеристика найдена лишь при условии, что зависимость от z определяется exp(-ihz), и в предположении существования режима отсечки, тогда эта зависимость относится к волне любого типа в полом металлическом волноводе с любым сечением.

Изобразим дисперсионную характеристику (см. рисунок 5.2). До 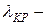область прозрачности т.к. .

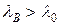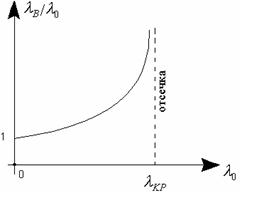
Рисунок 5.2 – Дисперсионная характеристика волновода

На этом участке фазовая и групповая скорость определяется выражениями:

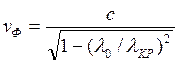; (5.4)

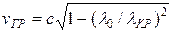. (5.5)

При этом фазовая скорость всегда больше скорости света, а групповая скорость всегда меньше скорости света. Их произведение на любой частоте.

Дата добавления: 2014-01-05