Математична постановка типових задач аналізу

Аналіз перехідних динамічних процесів є основним видом одноваріантного аналізу технічної системи. При цьому визначаються залежності фазових змінних від часу при заданих значеннях внутрішніх і зовнішніх параметрів.

MM, що описує динамічні властивості технічної системи, представляє собою сис-тему звичайних диференціальних рівнянь (ОДР). При цьому MM може бути отримана або в певній формі ОДР, або в нормальній формі Коші.

Неявна форма ОДР представляє динамічну поведінку технічної системи в загаль-ному вигляді: ,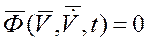

де, - вектор фазових змінних, достатніх для визначення стану модельованої технічної системи, розмірністю n; 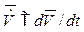- вектор похідних фазових змінних по часу, причому вектор 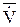має тільки 1 ненулевих елементів (1 < η); 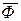- вектор функція; t - час. Початковими умовами є V_o = V | t = 0.

Частковим випадком вказаної системи рівнянь є MM, що описана ОДР в нормаль-ній формі Коші: ,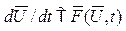

де, 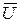- вектор змінних стану модельованої технічної системи, розмірністю n; 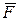- век-тор функція. Початковими умовами є 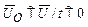. Аналіз динамічних процесів зво-диться до аналітичного або чисельного інтегрування ОДР.

Для більшості проектованих динамічних технічних систем перехідні процеси но-сять асимптотично стійкий характер, тобто при t → ∞ технічні системи переходить в певний стійкий стан. В зв’язку з цим дуже важливою задачею одноваріантного аналізу є розрахунок значень фазових змінних технічних систем в стійкому стані, тобто аналіз статичного режиму технічної системи. Іноді динамічний об’ект має декілька стійких станів і тоді необхідно розрахувати декілька його статичних режимів.

Аналіз статичного режиму можна здійснити, інтегруючи початкову систему ОДР на достатньо великому інтервалі часу (метод установлення). Це надійний, але не завжди ефективний метод.

В статиці похідні фазових змінних по часу дорівнюють нулю (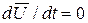) і від-сутні зміни в часі зовнішньої дії. Тому MM статичних станів можна виділити безпосе-редньо із MM динамічних процесів. В результаті отримаємо систему алгебраїчних рівнянь відносно відповідних змінних: .

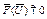Таким чином, одноваріантний аналіз статичних режимів технічних систем зводиться до розв'язку системи алгебраїчних рівнянь (АР) n-го порядку. Для розв'язку застосовують різні ітераційні методи.

В ряді областей техніки частина вихідних параметрів технічних систем визна-чається на основі аналізу частотних характеристик. При такому аналізі, як правило, допустима лінеаризація MM. Отже, система ОДР може бути представлена у вигляді:

,

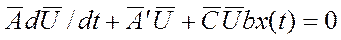де 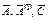- матриці з постійними або залежними від часу коефіцієнтами; 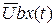- задана вектор-функція, що відображає зовнішні дії на об'єкт аналізу.

Задаючись синусоїдальною зовнішнєю дією на один із входів технічних систем і використовуючи для алгебраїзації вказаної лінійної системи ОДР перетворення Фур'є.

Розв'язок цієї системи звичайно здійснюється методом Гауса для ряду значень частоти w. Отримані залежності U(w) представляють собою частотні характеристики технічних систем, за якими визначають такі вихідні параметри, як резонансні частоти, полосу пропускання і т.д.

При проектуванні систем автоматичного управління важливе значення має задача динамічної стійкості. Аналіз стійкості може бути виконаний або безпосереднім інтег-руванням системи ОДР, або її дослідженням у відповідності із відомими критеріями стій-кості.

Найбільше розповсюдження при розрахунку лінійних систем отримали алгебраїч-ний критерій Гурвіца, частотні критерії за годографом Найквіста і за логарифміч-ними частотними характеристиками (ЛЧХ).

Аналіз чутливості полягає у визначенні впливу внутрішніх і зовнішніх параметрів

на вихідні параметрі, які називають коєфіціентами чутливості (впливу).

Статичний аналіз виконується з метою отримання інформації про розсіювання вихідних параметрів і розрахунку ймовірністі виконання умов працездатності при задан-них статистичних даних.

Дата добавления: 2014-01-05