Лекция 39. Натуральное число как результат измерения величины

План

1. Смысл натурального числа, полученного в результатеизмерения величины. Смыслсуммы и разности

2. Смысл произведения и частного натуральных чисел, полученных в результате измерения величин

77. Смысл натурального числа, полученного в результате измерения величины. Смысл суммы и разности

Выясняя смысл натурального числа как меры величины, все рассуждения будем вести на примере одной величины - длины отрезка.

Уточним сначала понятие «отрезок состоит из отрезков».

Определение. Считают, что отрезок х состоит из от­резков х₁, х₂ ,…, х_n, если он является их объединением и никакие два из них не имеют общих внутренних точек, хотя и могут иметь общие концы.

В этом же случае говорят, что отрезок х разбит на отрезки х₁, х₂ ,…, х_n и пишут х = х_{1 Å} х_{2 Å} х_я. Пусть задан отрезок х, его длину обозначим X. Выберем из множества отрезков некоторый отрезок е, назовем его единичным отрезком, а длину обозначим буквой Е.

Определение. Если отрезок х состоит из а отрезков, каждый из которых равен единичному отрезку е, то число а называют численным значением длины X данного отрезка при единице длины Е.

Пишут: X = а Е или а = т_Е(Х).

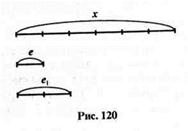
Например, отрезок х (рис: 120) состоит из 6 отрезков,
равных отрезку е. Если длину единичного отрезка обозначить буквой Е, а длину отрезка х буквой Х, то можно написать, что Х = 6 Е или 6 = т_Е(Х).

Из данного определения получаем, что ­что натуральное число как результат измерения длины отрезка (или как мера длины отрезка) показывает, из скольких единичных отрезков состоит отрезок, длина которого измеряется. При выбранной единице длины Е это число единственное.

В связи с таким подходом к натуральному числу сделаем два замечания:

1. При переходе к другой единице длины численное значение длины заданного отрезка изменяется, хотя сам отрезок остается неизменным. Так, если в качестве единицы длины выбрать дли­ну отрезка е₁, (рис. 120), то мера длины отрезка х будет равна числу 3. Записать это можно так: X = 3 ∙ Е ₁ или m_E (X) = 3.

2. Если отрезок х состоит из а отрезков, равных е, а отре­зок у - из b отрезков, равных е, то а = b тогда и только тогда, когда отрезки х и у равны.

Аналогично можно истолковать смысл натурального чис­ла и в связи с измерением других величин. Так, в записи 3 см² число 3 означает, что фигура F состоит из трех единичных квадратов с площадью, равной квадратному сантиметру,

Выясним теперь, какой смысл имеют сумма и разность натуральных чисел, полученных в результате измерения величин.

Теорема. Если отрезок х состоит из отрезков у и z и дли­ны отрезков у и z выражаются натуральными числами, то мера длины отрезка х равна сумме мер длин его частей.

Доказательство. Обозначим длины отрезков х, у и z со­ответственно буквами X, Y и Z. Пусть m(Y)=a, m(Z)=b при единице длины Е. Тогда отрезок у разбивается на а частей, каждая из которых равна отрезку длины Е, отрезок z разбива­ется на b таких частей. А потому весь отрезок х разбивается на а + b таких частей. Значит, т(X) = a + b = m(Y) + m(Z).

Из этой теоремы следует, что сумму натуральных чисел aub можно рассматривать как меру длины отрезка х, состоящего из отрезков у и z, мерами длин которых являются числа a u b.

a + b= m_E(Y)+m_E(Z) = m_E(Y + Z). Аналогичный смысл имеет сумма натуральных чисел, по­лученных в результате измерения других положительных ска­лярных величин.

Покажем, как используется данный подход к обоснованию выбора действия сложения при решении текстовых задач: «В саду собрали 7 кг смородины и З кг малины. Сколько всего килограммов ягод собрали?»

В задаче две величины - масса смородины и масса малины. Известны их численные значения. Требуется найти численное значение массы, которая получится, если данные массы сло­жить. Для этого, согласно рассмотренной теореме, надо сло­жить численные значения массы смородины и массы малины, т.е. получить выражение 7 + 3. Это математическая модель данной задачи. Вычислив значение выражения 7 + 3, получим ответ на вопрос задачи,

Теорема. Если отрезок х состоит из отрезков у и г и дли­ны Отрезков х и у выражаются натуральными числами, то мера длины отрезка z равна разности мер длин отрезков х и у.

Доказательство этой теоремы проводится аналогично до­казательству предыдущей.

Из этой теоремы следует, что разность натуральных чи­сел а и b можно рассматривать как меру длины такого от­резка z, что z Å у = х, если мера длины отрезка х равна а, мера длины отрезка у равна b.

a - b=m_E(X)- m_E(Y) = m_E(X-Y).

Аналогичный смысл имеет разность натуральных чисел, полученных в результате измерения других положительных скалярных величин.

Выясним, как используется данный подход к обоснованию выбора действия вычитания при решении текстовых задач, например, «Купили 7 кг картофеля и капусты. Сколько кило-, граммов картофеля купили, если капусты было 3 кг?»

В задаче рассматривается масса овощей, известно ее чис­ленное значение. Эта масса складывается из массы картофе­ля и массы капусты, численное значение которой также известно. Требуется узнать численное значение массы картофе­ля. Так как массу картофеля можно получить, вычитая из всей массы купленных овощей массу капусты, то численное значе­ние массы картофеля находят действием вычитания: 7-3. (Вычислив значение этого выражения, получим ответ на вопрос задачи.

При помощи сложения или вычитания решаются также текстовые задачи, в которых величины связаны отношением «больше на» или «меньше на». Например: «Купили 3 кг моркови, а картофеля на 2 кг больше. Сколько килограммов кар­тофеля купили?»

В задаче речь идет о двух величинах - массе моркови и массе картофеля. Численное значение первой массы известно, а численное значение второй надо найти, зная, что картофеля на 2 кг больше, чем моркови.

Если построить вспомогательную модель задачи, то можно сразу увидеть, что картофеля купили столько же, сколько моркови, и еще 2 кг, т.е. масса картофеля складывается из двух масс (З кг и 2 кг), и чтобы найти ее численное значение, надо сло­жить численные значения масс слагаемых. Получаем выраже­ние 3 + 2, значение которого и будет ответом на вопрос задачи.

Дата добавления: 2014-01-06