Понятие дроби

Лекция 49. Положительные рациональные числа

О РАСШИРЕНИИ МНОЖЕСТВА НАТУРАЛЬНЫХ ЧИСЕЛ

План:

1. Рациональные числа. Понятие дроби.

2. Рациональное число как класс эквивалентных дробей.

3. Арифметические действия над рациональными числами. Сумма, произведение, разность, частное рациональных чисел. Законы сложения и умножения.

4. Свойства отношения «меньше» на множестве рациональных чисел.

Действительные числа - не последние в ряду различных чисел. Процесс, начавшийся с расширения множества натуральных чисел, про­должается и сегодня - этого требует развитие различных наук и самой математики.

Знакомство учащихся с дробными числами происходит, как пра­вило, в начальных классах. Затем понятие дроби уточняется и расши­ряется в средней школе. В связи с этим учителю необходимо владеть понятием дроби и рационального числа, знать правила выполнения действий над рациональными числами, свойства этих действий. Все это нужно не только для того, чтобы математически грамотно ввести понятие дроби и обучать младших школьников выполнять с ними действия, но и, что не менее важно, видеть взаимосвязи множеств ра­циональных и действительных чисел с множеством натуральных чи­сел. Без их понимания нельзя решить проблему преемственности в обучении математике в начальных и последующих классах школы.

Отметим особенность изложения материала данного параграфа, которая обусловлена как небольшим объемом курса математики для учителей начальных классов, так и его назначением: материал будет представлен во многом конспективно, часто без строгих доказа­тельств; более подробно будет изложен материал, связанный с рацио­нальными числами.

Расширение множества N натуральных чисел будет происходить в такой последовательности: сначала строится множество Q+ положи­тельных рациональных чисел, затем показывается, как его можно расширить до множества R+ положительных действительных чисел, и, наконец, очень кратко описывается расширение множества R+ до множества R всех действительных чисел.

Пусть требуется измерить длину отрезка х с помощью единичного отрезка е (рис. 128). При измерении оказалось, что отрезок х состоит из трех отрезков, равных е, и отрезка, который короче отрезка е. В этом случае длина отрезка х не может быть выражена натуральным числом.

I—I—I—I—I—I—I—I—I—I—I—I—I—I—I

I—I—I—I—I

Рис. 128

Однако если отрезок е разбить на 4 равные части, то отрезок х окажется состоящим из 14 отрезков, равных четвертой части отрезка е. И тогда, говоря о длине отрезка х, мы должны указать два числа 4 и 14: четвертая часть отрезка е укладывается в отрезке точно 14 раз. Поэтому условились длину отрезка х записывать в виде 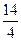∙ Е, где Е - длина единичного отрезка е, а символ 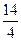называть дробью.

В общем виде понятие дроби определяют так.

Пусть даны отрезок х и единичный отрезок е, длина которого Е. Если отрезок х состоит из т отрезков, равных п-ой части отрезка е, то длина отрезка х может быть представлена в виде 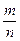∙ Е, где символ 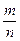называют дробью (и читают «эм энных»).

В записи дроби числа m и n - натуральные, m называется числителем, n - знаменателем дроби.

Дробь называется правильной, если ее числитель меньше знаменателя, и неправильной, если ее числитель больше знаменателя или равен ему.

Вернемся к рисунку 128, где показано, что четвертая часть отрезка уложилась в отрезке х точно 14 раз. Очевидно, это не единственный вариант выбора такой части отрезка е, которая укладывается в отрезке х целое число раз. Можно взять восьмую часть отрезка е, тогда отрезок х будет состоять из 28 таких частей и его длина будет выражаться дробью 28/8. Можно взять шестнадцатую часть отрезка е, тогда отрезок х будет состоять из 56 таких частей и его длина будет выражаться дробью 56/16.

Вообще длина одного и того же отрезка х при заданном единич­ном отрезке е может выражаться различными дробями, причем, если длина выражена дробью 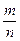, то она может быть выражена и любой дробью вида , где к - натуральное число.

Теорема. Для того чтобы дроб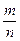и и 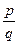выражали длину одного и того же отрезка, необходимо и достаточно, чтобы выполнялось равенство mq = пр.

Доказательство этой теоремы мы опускаем.

Определение. Две дроби m/n и p/q называются равными, если mq= n p.

Если дроби равны, то пишут m/n = p/q.

Например, 17/3 = 119/21, так как 17∙21 = 119∙3 = 357, а 17/19 23/27, потому что 17∙27 = 459, 19∙23 = 437 и 459 ¹ 437.

Из сформулированных выше теоремы и определения следует, что две дроби равны тогда и только тогда, когда они выражают длину одного и того же отрезка.

Нам известно, что отношение равенства дробей рефлексивно, сим­метрично и транзитивно, т.е. является отношением эквивалентности. Теперь, используя определение равных дробей, это можно доказать.

Теорема. Равенство дробей является отношением эквивалентности.

Доказательство. Действительно, равенство дробей рефлексивно: 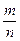= 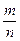, так как равенство

m/n = m/n справедливо для любых натуральных чисел т и п. Равенство дробей симметрично: если 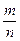=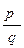, то 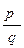= 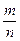, так как из тq= пр следует, что рп = qт (т, п, р, qÎN).

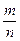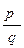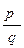Оно транзитивно: если = и = , то 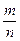= . В самом деле, так как, то тq = пр, а так как 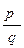= , то рs = qr. Умножив обе части равенства тq = пр на s, а равенства рs = qr на п, получим тqs = пр s и прs = qrп. Откуда тqs = qrп или тs = пr. Последнее равенство означает, что 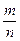= . Итак, равенство дробей рефлексивно, симметрично и транзитивно, следовательно, оно является отношением эквивалентности.

Из определения равных дробей вытекает основное свойство дроби. Напомним его.

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной.

На этом свойстве основано сокращение дробей и приведение дро­бей к общему знаменателю.

Сокращение дробей - это замена данной дроби другой, равной данной, но с меньшим числителем и знаменателем.

Если числитель и знаменатель дроби одновременно делятся только на единицу, то дробь называют несократимой. Например, - несократимая дробь, так как ее числитель и знаменатель делятся одновре­менно только на единицу, т.е. D(5, 17) = 1.

Приведение дробей к общему знаменателю - это замена данных дро­бей равными им дробями, имеющими одинаковые знаменатели. Общим знаменателем двух дробе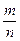й и 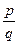является общее кратное чисел п и q, а наименьшим общим знаменателем - их наименьшее кратное К(п, q).

Задача. Привести к наименьшему общему знаменателю дроби и .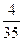

Решение. Разложим числа 15 и 35 на простые множители: 15 = 3∙5, 35 = 5∙7. Тогда К(15, 35) = 3∙5∙7= 105. Поскольку 105= 15∙7 = 35∙3, то ==, ==

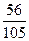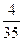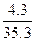Дата добавления: 2014-01-06