Множества натуральных чисел

Множество положительных рациональных чисел как расширение

Чтобы множество Q+ положительных рациональных чисел явля­юсь расширением множества N натуральных чисел, необходимо вы­полнение ряда условий.

Первое условие - это существование между N и Q+ отношения включения. Докажем, что

N Ì Q+.

Пусть длина отрезка х при единичном отрезке е выражается натуральным числом m. Разобьем единичный отрезок на п равных частей. Тогда n-ая часть единичного отрезка будет укладываться в отрезке Х точно mп раз, т.е. длина отрезка х будет выражена дробью 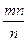. Значит, длина отрезка х выражается и натуральным числом m, и положительным рациональным числом 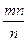. Но это

должно п быть одно и то же число. Поэтому целесообразно считать, что дроби вида 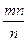являются записями натурального числа m.

Следовательно, N Ì Q+.

Так, например, натуральное число 6 можно представить в виде следующих дробей: 6/1 12/2, 18/3 24/4, 30/5 и т.д.

Отношение между множествами N и Q+ представлено на рисунке 129.

Рисунок 129.

Числа, которые дополняют множество на­туральных чисел до множества положительных рациональных, называются дробными.

Второе условие, которое должно быть выполнено при расширении множества натуральных чисел, - это согласованность операций, т.е. результаты арифметических дейст­вий, произведенных по правилам, существующим для натуральных чисел, должны совпадать с результатами действий над ними, но вы­полненных по правилам, сформулированным для положительных рациональных чисел. Нетрудно убедиться в том, что и это условие выполняется.

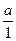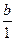Пусть а и b - натуральные числа, а + b - их сумма, полученная по правилам сложения в N. Вычислим сумму чисел а и b по правилу сложения в Q+. Так как а = , b = , то 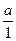+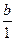= = 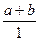а + b Убедиться в том, что второе условие выполняется и для других операций, можно аналогично.

Третье условие, которое должно быть выполнено при расшире­нии множества натуральных чисел - это выполнимость в Q+ опера­ции, не всегда осуществимой в N. И это условие соблюдено: деление, которое не всегда выполняется в множестве N, в множестве Q+ вы­полняется всегда.

Сделаем еще несколько дополнений, раскрывающих взаимосвязи между натуральными и положительными рациональными числами.

1. Черту в записи дроби 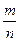— можно рассматривать как знак деления.

Действительно, возьмем два натуральных числа m и n и найдем их частное по правилу (4) деления положительных рациональных чисел:

m: n = := = .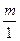

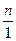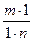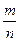Обратно, если дана дробь 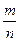, то ее можно рассматривать как част­ое натуральных чисел m и n:

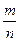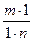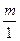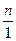==:= m: n.

2. Любую неправильную дробь можно представить либо в виде на­турального числа, либо в виде смешанной дроби.

Пусть 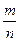- неправильная дробь. Тогда m > n. Если m кратно n, то в этом случае дробь 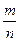является записью натурального числа. Если число m не кратно n, то разделим m на n с остатком:

m = nq + r, где r < n.

Подставим nq + r вместо m в запись 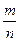и применим правило (1) сложения положительных рациональных чисел: 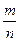= =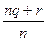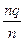+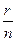= q + .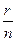

Так как r < n, то дробь 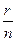- правильная. Следовательно, неправильная дробь — оказалась представленной в виде суммы нату­рального числа q и правильной дроби 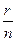. Это действие называется

выделением целой части из неправильной дроби. Например, 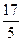==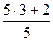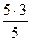+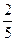=3+.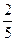

Сумму натурального числа и правильной дроби принято записывать без знака сложения: т.е. вместо

3 + 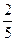пишут 3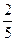и называют та­кую запись смешанной дробью.

Справедливо также утверждение: всякую смешанную дробь можно записать в виде неправильной дроби. Например:

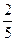3=3+=+==.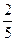

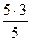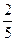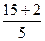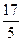Дата добавления: 2014-01-06