Этапы решения задачи на построение

Упражнения

1. Постройте с помощью циркуля и линейки сумму и разность двух данных: а) отрезков; б) углов.

2. Разделите данный угол на 4 равных части.

3. Дан треугольник АВС. Постройте другой, равный ему, треуголь­ник АВD.

4. Постройте окружность данного радиуса, проходящую через две данные точки.

Решение задачи на построение обычно включает четыре этапа:

анализ, построение, доказательство и исследование. Рассмотрим каж­дый из них в отдельности.

1. Анализ. На этом этапе осуществляется поиск решения задачи. Его конечная цель - установление последовательности, алгоритма, состоящего из основных или элементарных построений, приводящих к построению искомой фигуры. Как и решение геометрической задачи на вычисление и доказательство, поиск такого алгоритма сопровож­дается чертежом, иллюстрацией, помогающими установить связи и зависимости между данными и искомыми фигурами.

2. Построение. Этот этап решения представляет собой непосредст­венную реализацию на чертеже найденного алгоритма с помощью выбранных инструментов построения.

3. Доказательство. Его цель - доказательство того, что построен­ная на предыдущем этапе фигура действительно искомая, т.е. удовле­творяет всем поставленным в задаче условиям.

4. Исследование. Этот этап решения состоит в выяснении того, всег­да ли задача имеет решение; если не всегда, то при каких конкретных данных и сколько именно решений она имеет. При этом разными счи­таются решения, дающие неравные фигуры (или если и равные, то различно расположенные относительно фигуры, с которой связыва­лось построение).

Проиллюстрируем эти этапы на конкретном примере.

Задача. Построить параллелограмм по ос­нованию а, высоте h и одной из диагоналей d.

Согласно условию, данными являются отрез­ки, представляющие основание, высоту и диагональ параллелограмма (рис.). Все эти фигуры считаются уже построенными, и поэтому объяснение не требуется.

1. Анализ. Выполним чертеж-иллюстрацию, считая, что иско­мый параллелограмм АВС D уже построен (рис.). Отмечаем на чертеже данные элементы: ВС = а, ВН = h, DВ=d.

Устанавливаем связи и зависимости между элементами параллелограмма. От­мечаем, что противоположные стороны АВ и DС лежат на параллельных прямых, расстояние между которыми равно высоте h. Поэтому можно построить треугольник АВD и затем достроить его до параллело­грамма АВСD. Получим следующий алгоритм построения искомой фигуры:

1) Строим параллельные прямые МК и РQ на расстоянии h друг от друга.

2) На прямой МК откладываем отрезок АD = а.

3) Из точки D, как из центра, радиусом d проводим окружность и находим точку В ее пересечения с прямой РQ.

4) На луче ВQ откладываем отрезок ВС = а.

5) Строим отрезки АВ и СD.

2. Построение. Все этапы алгоритма построения выполняем циркулем и линейкой непосредственно на чертеже с использованием заданных элементов (рис. 157).

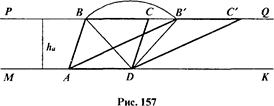
3. Доказательство. Рассмотрим четырехугольник АВСD. Его противоположные стороны АD и ВС параллельны, так как лежат на па­раллельных прямых МК и РQ. Эти же стороны равны по построению:

АD = ВС = а. Значит, АВСD - параллелограмм, у которого АD = а, ВD = d, а высота равна h, так как расстояние между параллельными прямыми МК и РQ равно h (по построению). Следовательно, АВСD -искомый параллелограмм.

4. Исследование. Проверим возможность построения паралле­лограмма АВСD непосредственно по шагам алгоритма построения.

1) Параллельные прямые МК и РQ на расстоянии h всегда можно построить, и притом единственным образом.

2) Построить отрезок АD = а на прямой МК также всегда можно, и притом единственным образом.

3) Окружность, проведенная из центра D радиусом d, будет иметь общие точки с прямой РQ только тогда, когда d ≥ h. Если d = h, то по­лучится одна общая точка В, если же d > h, то две общие точки В и В'.

5) Эти построения всегда однозначно выполнимы. Таким образом, решение возможно, если d ≥ h. Если d = h, то зада­ча имеет единственное решение, если же d > h, то два решения.

Дата добавления: 2014-01-06