Операції з класами

За допомогою логічних операцій з двох або кількох класів можуть бути утворені нові класи. До цих операцій належать:

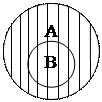
1. Операція об’єнання класів (додавання). Записується вона так: АÈВ. Об’єднувати можна класи, що знаходяться у будь-яких відношеннях один з одним:

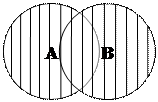(У першому випадку А - студенти, В – першокурсники, у другому випадку А – студенти, В – спортсмени).

2. Операція віднімання класів дає клас, який виключає елементи класів, що віднімаються.

Наприклад, якщо від класу «студенти» відняти клас «спортсмени», то залишаться студенти-неспортсмени.

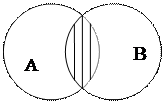3. Операція перетину класів (множення) полягає у відшуканні елементів, спільних для двох або кількох класів (множин). У нашому випадку це будуть студенти-спортсмени:

Операція перетину класів записується за допомогою знака множення: АÇВ.

Множина, отримана у результаті множення називається, також, як і в математиці, добутком. При множенні несумісних понять, наприклад, «слідчі» та «адвокати», виходить пустий (нульовий) клас.

4. Утворення доповнення (заперечення). Доповненням до класу А називається клас не-А (А¢), який при додаванні до А утворює універсальний клас (позначається знаком 1). Щоб утворити доповнення, треба з універсального класу виключити клас А:

1 – А = А¢

Для цього ми повинні визначити спочатку, до якого універсального класу належить даний клас. Наприклад, клас бухгалтерів належить до універсального класу економістів. Тепер, якщо виключити з класу економістів клас бухгалтерів, то ми отримуємо множину економістів-небухгалтерів. У своїй сумі обидва поняття утворюють універсальний клас економістів.

Щоб кожного разу не звертатися до кіл, треба запам’ятати деякі закони операцій над множинами.

Асоціативний закон:

(АÇВ)ÇС = АÇ(ВÇС) = АÇВÇС.

(АÈВ)ÈС = АÈ(ВÈС) = АÈВÈС.

1. Дистрибутивний закон:

АÇ(ВÈС) = (АÇВ)È(АÇС).

АÈ(ВÇС) = (АÈВ) Ç(АÈС).

2. Закон поглинання:

АÈ(АÇВ) = А.

АÇ(АÈВ) = А.

3. Закон де Моргана:

(АÇВ)¢ = А¢ÈВ¢.

(АÈВ)¢ = А¢ÇВ¢.

Дата добавления: 2014-01-06