Определение. Если каждому натуральному числу n поставлено в соответствие число хn, то говорят, что задана последовательность

С IV-V вв. нашей эры буква c, ранее обозначавшая звук [k], стала в некоторых позициях читаться как [ts].

Латинские согласные

Сейчас существуют два способа чтения буквы с - "классическое" (во всех случаях как - к), и "средневековое" (перед е, i, j, у, ае, ое - как русская буква ц; в иных случаях, перед согласными и в конце слова -как русская к). В России чаще употребляется второе чтение.

S - между гласными читается как "з ", в остальных случаях как "с ": rosa - роза, solus (солюс) - один.

L - принято читать мягко, как "ль".

Q, q - употребляется только в сочетании qu, которое читается как "кв ". Иногда так же читается и сочетание cu (i): aqua (аква) - вода, cuique (квиквэ) - каждому.

Сочетание su иногда также читается как "ев": svadeo (свадэо) - советую, suesco (свэско) - привыкаю.

Ti - перед гласными смягчается в "ци": ratio (рацио) - разум, initium (шшциум) - начало.

Однако в сочетаниях sti, xti, tti, sta, sto этого не происходит: Constituo (конституо) - постановлять, учреждать, bestia (бестиа) -зверь, mixtio (микстио) - смешение, Attica (аттика) - Аттика, consto (консто) - состоять, заключаться

x_1, х₂, …, х_n = {x_n}

Общий элемент последовательности является функцией от n.

x_n = f(n)

Таким образом последовательность может рассматриваться как функция порядкового номера элемента.

Задать последовательность можно различными способами – главное, чтобы был указан способ получения любого члена последовательности.

Пример. {x_n} = {(-1)ⁿ} или {x_n} = -1; 1; -1; 1; …

{x_n} = {sinpn/2} или {x_n} = 1; 0; 1; 0; …

Для последовательностей можно определить следующие операции:

1) Умножение последовательности на число m: m{x_n} = {mx_n}, т.е. mx₁, mx₂, …

2) Сложение (вычитание) последовательностей: {x_n} ± {y_n} = {x_n ± y_n}.

3) Произведение последовательностей: {x_n}×{y_n} = {x_n×y_n}.

4) Частное последовательностей: при {y_n} ¹ 0.

Ограниченные и неограниченные последовательности.

Определение. Последовательность {x_n} называется ограниченной, если существует такое число М>0, что для любого n верно неравенство:

т.е. все члены последовательности принадлежат промежутку (-М; M).

Определение. Последовательность {x_n}называется ограниченной сверху, если для любого n существует такое число М, что

x_n £ M.

Определение. Последовательность {x_n}называется ограниченной снизу, если для любого n существует такое число М, что

x_n ³ M

Пример. {x_n} = n – ограничена снизу {1, 2, 3, … }.

Определение. Число а называется пределом последовательности {x_n}, если для любого положительного e>0 существует такой номер N, что для всех n > N выполняется условие:

Это записывается: lim x_n = a.

В этом случае говорят, что последовательность {x_n} сходится к а при n®¥.

Свойство: Если отбросить какое- либо число членов последовательности, то получаются новые последовательности, при этом если сходится одна из них, то сходится и другая.

Пример. Предел последовательности lim .

Пример. При n®¥ последовательность 3, имеет пределом число 2.

Теорема. Последовательность не может иметь более одного предела.

Теорема. Если x_n ® a, то .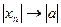

Теорема. Если x_n ® a, то последовательность {x_n} ограничена.

Следует отметить, что обратное утверждение неверно, т.е. из ограниченности последовательности не следует ее сходимость.

Например, последовательностьне имеет предела, хотя

Монотонные последовательности.

Определение. 1) Если x_n+1 > x_n для всех n, то последовательность возрастающая.

2) Если x_n+1 ³ x_n для всех n, то последовательность неубывающая.

3) Если x_n+1 < x_n для всех n, то последовательность убывающая.

4)Если x_n+1 £ x_n для всех n, то последовательность невозрастающая

Все эти последовательности называются монотонными. Возрастающие и убывающие последовательности называются строго монотонными.

Пример. {x_n} = 1/n – убывающая и ограниченная

{x_n} = n – возрастающая и неограниченная.

Пример. Последовательность {x_n}=монотонная возрастающая.

Пример. Последовательность {x_n} = монотонно убывает.

Следует отметить, что монотонные последовательности ограничены по крайней мере с одной стороны.

Теорема. Монотонная ограниченная последовательность имеет предел.

Число е.

Рассмотрим последовательность {x_n} = .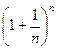

Число е является основанием натурального логарифма.

Выше представлен график функции y = lnx.

Предел функции в точке.

y f(x)

A + e

A

A - e

0 a - D a a + D x

Пусть функция f(x) определена в некоторой окрестности точки х = а (т.е. в самой точке х = а функция может быть и не определена)

Определение. Число А называется пределом функции f(x) при х®а, если для любого e>0 существует такое число D>0, что для всех х таких, что

0 < ïx - aï < D

верно неравенство ïf(x) - Aï< e.

То же определение может быть записано в другом виде:

Если а - D < x < a + D, x ¹ a, то верно неравенство А - e < f(x) < A + e.

Запись предела функции в точке:

Определение. Если f(x) ® A₁ при х ® а только при x < a, то - называется пределом функции f(x) в точке х = а слева, а если f(x) ® A₂ при х ® а только при x > a, то называется пределом функции f(x) в точке х = а справа.

у

f(x)

А₂

А₁

0 a x

Приведенное выше определение относится к случаю, когда функция f(x) не определена в самой точке х = а, но определена в некоторой сколь угодно малой окрестности этой точки.

Пределы А₁ и А₂ называются также односторонними пределами функции f(x) в точке х = а. Также говорят, что А – конечный предел функции f(x).

Предел функции при стремлении аргумента к бесконечности.

Определение. Число А называется пределом функции f(x) при х®¥, если для любого числа e>0 существует такое число М>0, что для всех х, ïхï>M выполняется неравенство

При этом предполагается, что функция f(x) определена в окрестности бесконечности.

Записывают: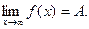

Графически можно представить:

y y

A A

0 0

x x

y y

A A

0 0

x x

Аналогично можно определить пределы для любого х>M и

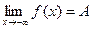для любого х<M.

Основные теоремы о пределах.

Теорема 1. , где С = const.

Следующие теоремы справедливы при предположении, что функции f(x) и g(x) имеют конечные пределы при х®а.

Теорема 2.

Доказательство этой теоремы будет приведено ниже.

Теорема 3.

Следствие.

Теорема 4. при

Теорема 5. Если f(x)>0 вблизи точки х = а и , то А>0.

Аналогично определяется знак предела при f(x) < 0, f(x) ³ 0, f(x) £ 0.

Теорема 6. Если g(x) £ f(x) £ u(x) вблизи точки х = а и , то и .

Определение. Функция f(x) называется ограниченной вблизи точки х = а, если существует такое число М>0, что ïf(x)ï<M вблизи точки х = а.

Теорема 7. Если функция f(x) имеет конечный предел при х®а, то она ограничена вблизи точки х = а.

Бесконечно малые функции.

Определение. Функция f(x) называется бесконечно малой при х®а, где а может быть числом или одной из величин ¥, +¥ или -¥, если .

Бесконечно малой функция может быть только если указать к какому числу стремится аргумент х. При различных значениях а функция может быть бесконечно малой или нет.

Пример. Функция f(x) = xⁿ является бесконечно малой при х®0 и не является бесконечно малой при х®1, т.к. .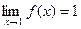

Теорема. Для того, чтобы функция f(x) при х®а имела предел, равный А, необходимо и достаточно, чтобы вблизи точки х = а выполнялось условие

f(x) = A + a(x),

где a(х) – бесконечно малая при х ® а (a(х)®0 при х ® а).

Свойства бесконечно малых функций:

1) Сумма фиксированного числа бесконечно малых функций при х®а тоже бесконечно малая функция при х®а.

2) Произведение фиксированного числа бесконечно малых функций при х®а тоже бесконечно малая функция при х®а.

3) Произведение бесконечно малой функции на функцию, ограниченную вблизи точки х = а является бесконечно малой функцией при х®а.

4) Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю есть величина бесконечно малая.

Дата добавления: 2014-01-06