Перестановки без единичных циклов

Каково число перестановок из n элементов, каждая из которых состоит из k циклов, отличных от единичных.

Ясно, что ответ на этот вопрос по самому определению функции С_n дается коэффициентом при t^k в выражении для С_n(0, t,…, t), или для краткости d_n(t). На основании соотношения (3а)

exp(ud(t))= = exp(t(u²/2+u³/3+…) =(1-u)^-t exp(-tu) (5)

откуда, сравнивая с (4), получаем

d_n(t)= 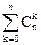C_n-k(t)(-t)^k, (6)

где C₀(t)=1, C_n(t)=t(t+1)…(t+n-1), n>0, как и ранее.

Тогда если

d_n(t)=,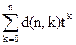

то соотношение для коэффициентов, вытекающее из (6), окажется следующее:

d(n,k)= 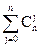(-1)^j C(n-j,k-j) (7)

Ввиду (7) числа d(n,k) называются присоединенными числами Стирлинга первого рода. Следует отметить, что соотношением, двойственным соотношению (6), полученным умножением (5) на e^tu и приравниванием коэффициентов при uⁿ является

C_n(t)= 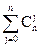d_n-j(t)(t)^j.

Последний результат соответствует любопытному представлению чисел Стирлинга

С(n,k)= 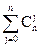(-1)^j d(n-j,k-j). (8)

Теперь полученный ответ формально является полным, однако существуют более простые зависимости. Так путем дифференцирования (5) по u получаем [ при обычном условии d(t)ⁿ≡d_n(t)], что

d(t)exp(ud(t))=−t exp(ud(t))+t(1−u)^-1exp(ud(t)) (9)

или

(1−u)d(t)exp(ud(t))=tu exp(ud(t)).

Это соответствует соотношению

d_n+1(t)=n d_n(t)+ntd_n-1(t), (10)

что в свою очередь соответствует простому рекуррентному соотношению

d(n+1,k)=nd(n,k) +nd(n-1,k-1), (11)

которое также может быть получено простым комбинаторным рассуждением.

Разбиение чисел. [2]

Пусть n – натуральное число и n=b₁+b₂+…+b_k, где k, b₁,b₂,…,b_k>0, при этом будем считать суммы эквивалентными, если они отличаются только порядком слагаемых. Класс эквивалентных сумм можно представить однозначно последовательностью a₁,a₂,…,a_k, где a₁≥a₂≥…≥a_k, и числа a₁,a₂,…,a_k являются числами b₁,b₂,…,b_k, упорядоченными по невозрастанию. Каждую такую последовательность a₁,a₂,…,a_k будем называть разбиением числа n на k слагаемых.

Замечание. Если в сумме b₁+b₂+…+b_k порядок слагаемых считается существенным, то такие представления числа n обычно называются композицией числа n на k слагаемых.

Число разбиений числа n на k слагаемых будем обозначать P(n,k), а число всех разбиений числа n (на произвольное число слагаемых) – через P(n). Очевидно,

P(n)=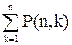, n>0.

Положим, P(0,0)=P(0)=1.

Теорема 1. P(n,k) равно числу разбиений числа n c наибольшим слагаемым равным k.

Доказательство.

Рассмотрим способ представления разбиения числа в виде диаграмм Ферреса (Феррера):

Она состоит для разбиения n= a₁+a₂+…+a_k из k строк, i^-я строка содержит a_i точек.

Пример 16=6+4+4+2

· · · · · · · · · ·

· · · · · · · ·

· · · · · · · сопряженное разбиение

· · · · ·

·

·

Каждому разбиению числа n однозначно соответствует сопряженное разбиение этого числа, которое получается транспонированием диаграммы Ферреса. Отсюда следует, что транспонирование диаграммы Ферреса определяет взаимно однозначное соответствие между разбиениями числа n на k слагаемых и разбиением числа n с наибольшим слагаемым, равным k.

Теорема 2. Число разбиений числа n на попарно различные слагаемые равно числу разбиений числа n на нечетные слагаемые.

Доказательство (соответствие Глейшера).

Установим взаимно однозначное соответствие между разбиениями, о которых идет речь в теореме.

Пусть n разбито на нечетные слагаемые b₁,b₂,…,b_p, где b_i появляется в разбиении r_i раз, 1≤i≤p. Положим r_i=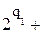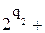… (q₁>q₂>….).

Произведем замену r_i слагаемых b_i на попарно различные слагаемые

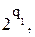b_ib_i…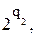

т. е.

r_i b_i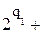= b_ib_i…,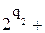

Повторяя эту замену для каждого i, 1≤i≤p, и упорядочивая слагаемые по невозрастанию, получаем в результате разбиение числа n на попарно различные слагаемые. (Здесь использована теорема об однозначном представлении каждого натурального числа в виде произведения нечетного числа на степень числа два.)

Пример.

26=7+5+5+3+3+1+1+1: 7·2⁰+5·2¹+3·2¹+1·(2¹+2⁰)=7+10+6+2+1=10+7+6+2=1

И обратно,

Пусть n=b₁+b₂+…+b_k, где 0 <b_k,…<b₁, тогда b_i= p·2^q, 1≤i≤p.

Заменяем каждое b_i на 2^q слагаемых p, затем упорядочиваем по невозрастанию, получаем разбиение n на сумму нечетных слагаемых.

Таким образом, описанное преобразование определяет взаимно однозначное соответствие между разбиениями на нечетные слагаемые и разбиениями на попарно различные слагаемые.

Теорема 3. Число разбиений числа n, в котором ни одно из слагаемых не превосходит k, равно числу разбиений числа n+k на k слагаемых, т. е. P(n+k,k).

Доказательство.

Пусть δ – разбиение числа n, в котором ни одно из слагаемых не превосходит k, a δ′ сопряженное с δ, тогда δ′ содержит не более k слагаемых. Пусть δ′=(b₁,b₂,…,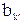), k′≤k, тогда разбиение (k,b₁,b₂,…,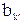) является разбиением числа n+k ровно на k слагаемых. Заметим, что (k,b₁,b₂,…,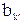) определяется однозначно через δ.

Пусть ε= (b₁,b₂,…,b_k) разбиение n+k на k слагаемых, а ε′ – разбиение сопряженное с ε′. Пусть ε′=(k,b₁,b₂,…,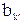), тогда (b₁,b₂,…,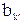), разбиение числа n, при этом (b₁,b₂,…,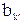) определяется однозначно. Теорема доказана!

Теорема 4. Число разбиений числа а–с равно с b–1 частями, не превосходящими с, равно числу разбиений числа a–b с c–1 – частями, не превосходящими b.

Доказательство.

Рассмотрим графическое представление типичного разбиения первого типа и преобразуем это разбиение следующим образом: добавим новую строку из c точек, затем удалим первый столбец (который теперь имеет b точек) и произведем сопряжение полученного разбиения:

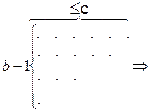
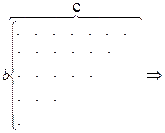
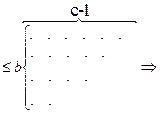
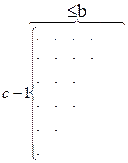
сразу видно, что такое последовательное преобразование представляет собой взаимно однозначное соответствие между этими двумя типами разбиений и, следовательно, доказывает теорему.

В качестве примера рассмотрим случай a=14, b=5, c=4:

4+4+1+1→3+3+3

4+3+2+1→4+3+2

4+2+2+2→5+2+2

3+3+3+1→4+4+3

3+3+3+2→5+3+1

Введем производящие функции, которые применяются в некоторых задачах, связанных с разбиением чисел.

Пусть n=a₁+a₂+…+a_k, тогда <λ₁, λ₂,…, λ_n>, где λ_i=|{(j:a_j=i)&(1≤j≤k)}|. Имеем, очевидно,

,

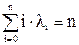и каждая последовательность<λ₁, λ₂,…, λ_n>, (λ₁, λ₂,…, λ_n≥0), отвечающая этому условию однозначно определяет разбиение числа n, содержащее λ_i слагаемых равных i, 1≤j≤n.

Обозначим, P_h(n) – число разбиений числа n на слагаемые не превышающие h, а P(n) определяет число всех разбиений числа n.

Теорема 4. Производящая функция для последовательности P_h(0), P_h(1), P_h(2),… равна

(1+t+t²+t³+…)(1+t²+t⁴+t⁶+…)…(1+t^h+t^2h+t^3h+…)=(1-t)^-1(1-t²)^-1…(1-t^h)^-1.

Доказательство.

Согласно определению произведения h рядов с правой стороны является суммой слагаемых вида 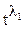··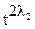…·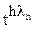(λ_i – номер члена выбранного из i-го ряда). Таким образом, коэффициент при tⁿ равен числу последовательностей <λ₁, λ₂,…, λ_n>, таких что 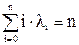, а, следовательно, в соответствие с предыдущими замечаниями он равен P_h(n).

Аналогичным образом доказывается следующая теорема:

Теорема 6. Производящая функция для последовательности P(0), P(1), P(2),… равна

(1+t+t²+t³+…)(1+t²+t⁴+t⁶+…)…(1+t^h+t^2h+t^3h+…)…=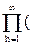1-t^h)^-1.

Замечание. В этом месте следовало бы строго определить ряд, являющийся бесконечным произведением рядов F₁(t)·F₂(t)·F₃(t)·…. Обозначим I_n(t) “частичное” произведение F₁(t)·F₂(t)·…·F_n(t) и через p_n – наименьшую ненулевую степень с ненулевым коэффициентом в F_n(t). Положим, что коэффициент при нулевой степени в каждом из рядов F_n(t) равен единице, и что 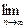p_n=∞ (оба эти условия выполнены в условии теоремы). Тогда коэффициент при tⁿ в I_m(t) один и тот же для всех m, больших некоторого числа m_n. Именно этот коэффициент принимается как коэффициент при tⁿ в ряде, определенном бесконечным произведением F₁(t)·F₂(t)·F₃(t)·….

Техника производящих функций позволяет провести простые доказательства некоторых свойств разбиений числа. Приведем в качестве примера другое доказательство теоремы 2.

Пусть R(t) – производящая функция для разбиений на попарно различные слагаемые, тогда

R(t)=(1+t)(1+t²)(1+t³) ·…·(1+t^k)·…,

а производящая функция для разбиений на нечетные слагаемые равна

N(t)=(1-t)^-1(1-t³)^-1·…·(1-t^2k-1)^-1·….

(заметим, что оба произведения абсолютно сходящиеся при 0<t<1)

Пользуясь зависимостью 1+t^k=(1-t^2k)/(1-t^k), получаем

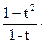
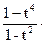
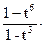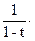
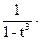
R(t)=…=…=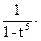N(t)

Теорема 7. Пусть P_e(D,n) (соответственно P_о(D,n)) число разбиений n на четное (соответственно нечетное) число различных частей[3]. Тогда

P_e(D,n)− P_о(D,n)=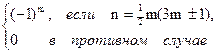

Доказательство.

Мы попытаемся установить взаимно однозначное соответствие между разбиениями, перечисляемыми функцией P_e(D,n), и разбиениями, перечисляемыми функцией P_о(D,n). Для большинства целых n наша попытка увенчается успехом; однако, если n является одним из пятиугольных чисел 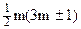, то это и составит единственный исключительный случай.

Введем два параметра разбиения α= (a₁,a₂,…,a_k): s(α)=a_k (наименьшая часть разбиения α) и σ(α) – наибольшее j, для которого a_j=a₁-j+1 (при αÎ D – число членов в монотонно убывающей последовательности с разницей между соседними членами, равной 1, начинающейся с a₁ и состоящей из первых частей разбиения α). Графически эти параметры описываются очень просто:

α=(7 6 4 3 2) α=(8 7 6 5)

...............

.............

.... σ(α)=2...... σ(α)=4

........

.. s(α)=5

s(α)=2

Преобразуем разбиение следующим образом.

Случай 1. s(α) ≤ σ(α). В этом случае увеличение на единицу каждую из s(α) наибольших частей α и отбрасываем наименьшую часть. Таким образом

α=(7 6 4 3 2) → (8 7 4 3),

т. е.

...............

.............

.... →....

......

..

Случай 2. s(α) > σ(α). В этом случае, наоборот, уменьшаем на единицу каждую из σ(α) наибольших частей α и образуем наименьшую часть величины σ(α). Таким образом

α=(8 7 4 3) → (7 6 4 3 2),

т. е.

................

..............

.... →....

......

..

Описанная процедура в обоих случаях меняет четность числа частей разбиения; замечая, что к разбиению можно применять лишь один из этих случаев, видим, что такое отображение устанавливает взаимно однозначное соответствие. Однако имеются определенные разбиения, для которых это отображение не работает, например, α=(8 7 6 5). К нему нужно было бы применять случай 2, но получаемое посредством него новое разбиение уже содержит одинаковые части, т. е. не принадлежит нашему множеству D. Итак, случай 2 не работает, когда разбиение имеет вид σ(α)=r, s(α) =r+1, и в этом случае само разбиваемое число, очевидно, равно

(r+1)+(r+2)+…+2r=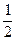r(3r+1).

С другой стороны, случай 1 не работает, когда разбиение имеет r частей, σ(α)=r, s(α) =r, а само разбиваемое число, очевидно, равно

r+(r+1)+…+(2r-1)=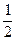r(3r-1).

Таким образом, если n не является пятиугольным числом, то P_e(D,n)=P_о(D,n), а если n= 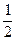r(3r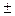1), то P_e(D,n) = P_о(D,n)+(-1)^r

Следствие 1. (Пентагональная теорема Эйлера).

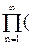1-tⁿ) = 1+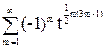(1+t^m)= .

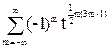Доказательство.

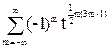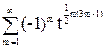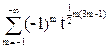=1+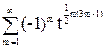+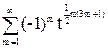=1++=1+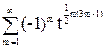(1+t^m)=1+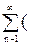P_e(D,n) - P_о(D,n))tⁿ_.

Для полноты доказательства нужно еще показать, что

1+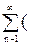P_e(D,n) - P_о(D,n))tⁿ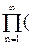_.= 1-tⁿ).

Теперь

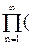1-tⁿ)= …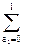

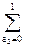
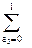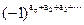
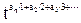
как и в доказательстве формулы теоремы 5. Заметим, каждое разбиение с различными частями подсчитывается с весом 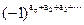, который равен +1, если это разбиение имеет четное число частей, и -1 в случае нечетного числа частей. Следовательно,

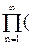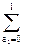
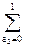
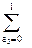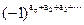
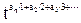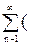1-tⁿ)= …=1+P_e(D,n) - P_о(D,n))tⁿ

и тем самым имеем требуемое.

Следствие 2. (Эйлер). Если n>0, то

P(n)–P(n–1)–P(n–2)+P(n–5)+P(n–7)+…

…+(-1)^m P(n–m(3m-1)/2)+(-1)^m P(n–m(3m+1)/2)=0, (*)

где P(M)= 0 для всех отрицательных M.

Доказательство.

Пусть а_n обозначает левую часть равенства (*). Тогда

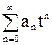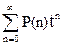=[1+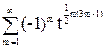(1+t^m)]= 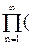1-tⁿ)^-1∙ 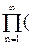1-tⁿ)=1,

где предпоследнее равенство сразу следует из 6 и следствия1. поэтому а_n = 0, для n>0.

Следствие 2 представляет собой весьма эффективный алгоритм для вычисления P(n).

Значения P(n) растут очень быстро с ростом n. Имеем:

P(1)=1; P(2)=2; P(3)=3; P(4)=5; P(5)=7; P(6)=11; P(10)=42; P(20)=627; P(50)=204 226; P(100)=190 569292; P(200)=3 972 999 029 388.

Однако, имеется точная формула для P(n) – результат, выведенный Харди и Рамануджаном и усовершенствованный Радемахером. Этот результат относится к одному из высших достижений теории разбиений:

Теорема (Харди – Рамануджана – Радемахера).

P(n)=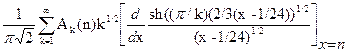, (1)

где

А_k(n)=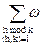_h,ke^-2πinh/k

и ω_h,k – корень 24k-й степени из единицы, определяемый специальным образом.

Это необычайное тождество, котором левой частью служит простая арифметическая функция P(n), а в правой – бесконечный ряд, включающий в себя π, квадратные корни, комплексные корни из единицы и производные гиперболических функций, являет собой не только чисто теоретическую формулу для P(n), но формулу, обеспечивающую действительно быстрое вычисление.[4] (Для малых значений n можно, конечно, пользоваться рекуррентностью из приведенной ниже пентагональной теоремы Эйлера.) Кроме того, довольно просто показать, что каждый член бесконечного ряда в (1) есть O(exp{π(2n)^1/2/k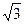}). Следовательно, первый член k=1 дает нам асимптотическую формулу для P(n); замечая, что A₁(n)=1, без особых трудностей получаем, что при n→∞

P(n)≈.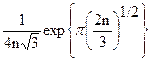

Задачи.

1. (Саббарао). Число разбиений числа n, в которых части встречаются дважды, трижды или по пять раз, равно числу разбиений n на части, сравнимые с 2, 3, 6, 9, 10 по модулю 12.

2. Число разбиений числа n, в которых могут повторяться только нечетные части, равно числу разбиений n в которых нет части, встречающейся более чем три раза.

3. (Сильвестр). Число разбиений числа n с различными нечетными частями равно числу разбиений n, которые являются самосопряженными (т. е. совпадают со своим сопряжением).

4. (Эйлер). Абсолютное значение излишка числа разбиений n с нечетным числом частей над числом разбиений n с четным числом частей равно числу разбиений n на различные нечетные части.

Дата добавления: 2014-01-06