
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Показательный (экспоненциальный) закон распределения
|
|
|
|
Показательное распределение является частным случаем распределения Эрланга при k = 0.
Показательным (экспоненциальным ) называют распределение вероятностей непрерывной случайной величины X. которое описывается плотностью
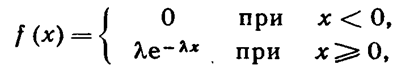 |
(3.1)
где λ – постоянная положительная величина.
Из выражения (3.1), следует, чтопоказательное распределение определяется одним параметром λ.
Эта особенность показательного распределения указывает на его преимущество по сравнению с распределениями, зависящими от большего числа параметров. Обычно параметры неизвестны и приходится находить их оценки (приближенные значения) разумеется, проще оценить один параметр, чем два или три и т. д. Примером непрерывной случайной величины, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока.
Найдем функцию распределения показательного закона.
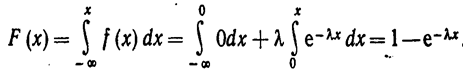
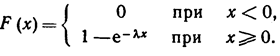 Итак
Итак
(3.2)
Графики плотности и функции распределения показательного закона изображены на рис. 3.1.
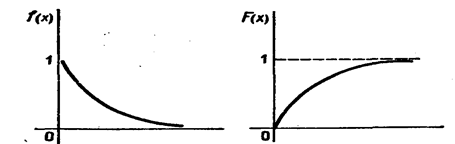 |
Рис.3.1.Графики плотности и функции распределения показательного закона
Найдем вероятность попадания в интервал (а, b ) непрерывной случайной величины X, которая распределена по показательному закону, заданному функцией распределения
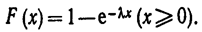
Используем известную формулу вычисления вероятности попадания случайной величины в заданный интервал, а именно:
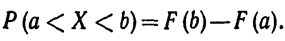 |
Учитывая, что 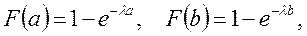 получим:
получим:
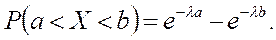 (3.3)
(3.3)
Значения функции 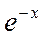 можно находить по таблице.
можно находить по таблице.
Числовые характеристики показательного распределения
Пусть непрерывная случайная величина Χ распределена по показательному закону
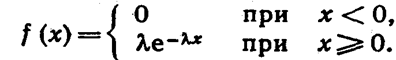
Найдем математическое ожидание, используя формулу её вычисления для непрерывной случайной величины:
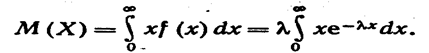 |
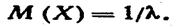 Интегрируя по частям, получим
Интегрируя по частям, получим
(3.4)
Таким образом, математическое ожидание показательного распределения равно обратной величине параметра λ.
Найдем дисперсию, используя формулу её вычисления для непрерывной случайной величины:
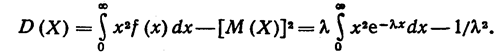
Интегрируя по частям, получим
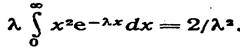 |
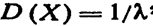 Следовательно:
Следовательно:
(3.5)
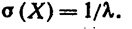 Найдем среднее квадратическое отклонение, для чего извлечем квадратный корень из дисперсии:
Найдем среднее квадратическое отклонение, для чего извлечем квадратный корень из дисперсии:
(3.6)
Сравнивая (3.4), (3.5) и (3.6), видно, что
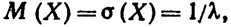 (3.7)
(3.7)
т. е. математическое ожидание и среднее квадратическое отклонение показательного распределения равны между собой.
Показательное распределение широко применяетсяв различных приложениях финансовых и технических задач, например, в теории надежности.
4. Распределение «хи-квадрат» и распределение Стьюдента.
4.1 Распределение «хи-квадрат» ( 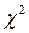 - распределение)
- распределение)
Пусть Χi (ί = 1, 2,..., n)—нормальные независимые случайные величины, причем математическое ожиданиекаждой из нихравно нулю, а среднее квадратическое отклонение — единице.
Тогдасумма квадратов этих величин
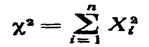
распределена по закону 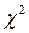 с
с 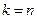 степенями свободы, если же эти величины связаны одним линейным соотношением, например
степенями свободы, если же эти величины связаны одним линейным соотношением, например 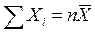 , то число степеней свободы
, то число степеней свободы 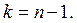
Распределение хи-квадрат нашло широкое применение в математической статистике.
Плотность этого распределения
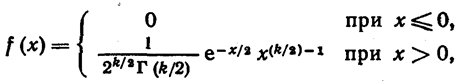 |
(4.1)
где 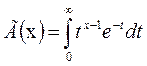 - гамма-функция, в частности
- гамма-функция, в частности 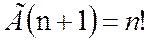 .
.
Отсюда видно, чтораспределение хи-квадрат определяется одним параметром — числом степеней свободы k.
С увеличением числа степеней свободыраспределение хи-квадрат медленно приближается к нормальному.
Хи-квадрат распределение получается, если в законе распределения Эрланга принять λ = ½ и k = n /2 – 1.
Математическое ожидание и дисперсия случайной величины, имеющей хи-квадрат распределение, определяются простыми формулами, которые приведем без вывода:
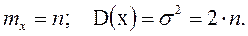 (4.2)
(4.2)
Из формулы следует, что при 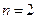 хи-квадрат распределение совпадает с экспоненциальным распределением при λ = ½.
хи-квадрат распределение совпадает с экспоненциальным распределением при λ = ½.
Интегральная функция распределения при хи-квадрат распределенииопределяетсячерез специальные неполные табулированные гамма-функции 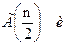
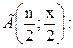
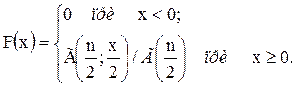 |
(4.3)
Применение системы уравнений (4.3), использующей табулированные (табличные) неполные гамма-функции, позволяет определить вероятность попадания случайной величины в заданный интервал, имеющей хи-квадрат распределение.
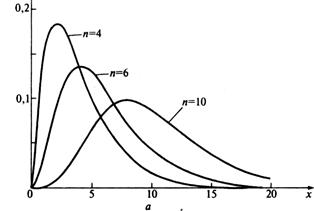
|
Рис.4.1. а) Графики плотности вероятности при хи-квадрат распределении
Графики плотности вероятности при хи-квадрат распределении

Рис.4.1. б) Графики функции распределения при хи-квадрат распределении
Графики функции распределения при хи-квадрат распределении
4.2 Распределение Стьюдента
Пусть Z – нормальная случайная величина, причём 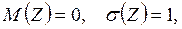
а V – независимая от Z величина, которая распределена по закону хи-квадрат с k степенями свободы.Тогда величина:
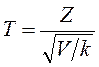 |
(4.4)
имеет распределение, которое называют t -распределением или распределением Стьюдента (псевдоним английского статистика В. Госсета),
с k = n - 1 степенями свободы ( n - объём статистической выборки при решении задач статистки).
Итак, отношение нормированной нормальной величинык квадратному корню из независимой случайной величины, распределенной по закону «хи квадрат» с k степенями свободы, деленной на k, распределено по закону Стьюдента с k степенями свободы.
Плотность распределения Стьюдента:
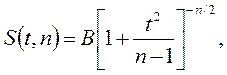 |
(4.5)
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 5040; Нарушение авторских прав?; Мы поможем в написании вашей работы!