Эйлеровы графы. Степенью вершины v (обозначается deg v) в графе G называется число ребер, инцидентных вершине v

Степенью вершины v (обозначается deg v) в графе G называется число ребер, инцидентных вершине v. Граф, каждая вершина v, которого имеет четную степень, называется четным. Эйлеров граф – это связный четный граф.

Пусть W_p – число помеченных четных графов порядка p. Тогда справедлива следующая теорема:

Теорема. Число помеченных четных графов порядка p равно числу помеченных графов порядка p-1:

W_p=.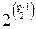

Доказательство.

Чтобы доказать этот результат, мы сейчас установим взаимно однозначное соответствие между этими двумя графов. Рассмотрим произвольный граф порядка p-1. Граф G должен иметь четное число вершин нечетной степени. Добавим к нему вершину v, которой припишем пометку p. Наконец, из графа G и вершины v строим граф G′, имеющей нечетную степень. Этот граф G′ является помеченным четным графом порядка p. Легко видеть, что описанное соответствие является взаимно однозначным и что каждый помеченный четный граф порядка p может быть получен таким способом из некоторого помеченного графа порядка p-1.

Чтобы получить формулу для числа помеченных эйлеровых графов, мы будем использовать производящие функции. Итак, пусть W(t) – экспоненциальная производящая функция для помеченных четных графов, такая что

W(t) =t^p/p! (10)

Далее, пусть U_p – число помеченных эйлеровых графов порядка p, так что

U(t) =t^p/p! (11)

является соответствующей экспоненциальной производящей функцией.

Теорема. Экспоненциальная производящая функция U(t) для помеченных эйлеровых графов удовлетворяет соотношениям

U(t) =ln(W(t)+1) (12)

и

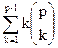
U_p= -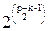U_k. (13)

Формула (12) следует из того факта, упомянутого после равенства (8), что если известна производящая функция для произвольного класса графов, то производящая функция для соответствующих связных графов получается с помощью формального логарифмирования первого ряда. Рекуррентное соотношение (13) для U_p является следствием формул (12) и (9).

Для нескольких первых членов ряда U(t) имеем равенство

U(t)=t+t³/3!+ 3t⁴/4!+ 38t⁵/5!+… (14)

Упражнение. Проверьте справедливость равенства (14).

К несколько более трудной относится задача – определение числа помеченных эйлеровых графов с заданным числом вершин и ребер, установленный Ридом.

Теорема [7]. Многочлен w_p(t), у которого коэффициент при t^q равен числу помеченных графов имеющих p вершин четной степени и q ребер, задается формулой

w_p(t)= 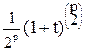. (15)

Для малых значений p находим, что (проверьте):

W₁(t)= w₂(t)=1 w₃(t)=1+t³ w₄(t)=1+4t³+ 3t⁴.

Дата добавления: 2014-01-06