Формула Томсона

Дослід показує, що зі збільшенням значення активного опору контура амплітуда коливань швидко зменшується, коливання значно швидше припиняються. Однак активний опір на частоту коливань помітно не впливає (нижче побачимо, що такий вплив все-таки є). На практиці для визначення частоти коливань у коливальному контурі часто користуються формулою Томсона (1853 p.):

де f— частота коливань, Гц; Т— період коливань, с; L — індуктивність, Гн; С — ємність, Ф. Ці формули цілком придатні і для більшості випадків практики З останнього досліду можна зробити важливий висновок: не завжди в електричному колі, яке складається з котушки і конденсатора, можливі електромагнітні коливання. Якщо опір електричного кола досить значний, то після заряджання конденсатора він розрядиться через котушку зі значним опором. Однак при цьому енергія електричного поля конденсатора перетвориться на теплоту і конденсатор унаслідок явища самоіндукції не перезарядиться. Матиме місце так зване аперіодичне розряджання конденсатора.

Встановимо умови, за яких коливання можливі, а за яких — ні. Однак для цього потрібно докладно проаналізувати явища в коливальному контурі з використанням математичного апарату. Уявімо собі коливальний контур, до складу якого входить конденсатор С, котушка L та активний опір R (мал. 3.6). Нехай у певний момент часу конденсатор зарядили до напруги U і від'єднали зовнішнє джерело живлення. Якби в електричному колі був лише резистор R, то струм протікав би лише доти, доки потенціали обкладок конденсатора не зрівнялися. Якщо ж у колі є котушка з індуктивністюL, то в той момент, коли потенціали обкладок конденсатора зрівняються, електрорушійна сила самоіндукції, що виникає в котушці при зміні сили струму в ній, підтримає струм, який зменшується, і відбудеться перезарядження обкладок конденсатора. Після цього струм у контурі йтиме у протилежному напрямку, конденсатор знову перезарядиться і т. д. Виникають електромагнітні коливання, які ми вже дослідили експериментально. Оскільки частина енергії втрачається, то коливання затухають і з часом припиняються зовсім. В електричних колах з індуктивністю, ємністю та активним опором електромагнітні коливання можуть і не виникнути при певних співвідношеннях між згаданими величинами (L, С, R). У реальних контурах (із втратами енергії) період електромагнітних коливань визначається за формулою: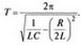

Ідеальними вважають контури, в яких немає втрат електромагнітної енергії. Для цього випадкуR = 0 і формула переходить у формулу Томсона, цілком придатну для більшості практичних випадків. Остання формула дає змогу зробити важливий висновок: за яких умов коливання в досліджуваному колі можливі. Значення періоду коливань має бути додатним числом і не може бути нескінченно великим. Тож у формулі знаменник має бути більшим за нуль. Отже, 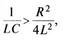або .

Лише за цих умов коливання в колі можливі і коло можна вважати коливальним контуром.

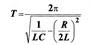. Якщо R = 0 (ідеальний контур), то 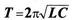формула Томсона.

Обов'язкова умова можливості виникнення вільних електромагнітних коливань .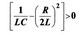

Під час вільних коливань у контурі між напругою і силою струму встановлюється певне співвідношення, яке визначається параметрами контура. Сила струму в двох контурах за однакової амплітуди напруга може бути різною. Тому контур характеризують так званим хвильовим (або характеристичним) опором.

Якщо знехтувати втратами енергії в контурі, то можна вважати, шо максимальне значення енергії магнітного поля котушки дорівнює максимальному значенню енергії електричного поля конденсатора: Звідси можна знайти співвідношення між амплітудою сили струму й амплітудою напруги: . Вираз має розмірність опору.

Це і є хвильовий або характеристичний опір.

Щоб з'ясувати фізичний зміст характеристичного опору, розглянемо два контури, частоти власних коливань яких однакові, а конденсатори різних ємностей, наприклад С₁< C₂. Обидва конденсатори заряджаються до однакової напруги, але в першому контурі запас енергії менший, ніж у другому. Відповідно, й амплітуда сили струму в першому контурі буде менша. Тому вважають, що хвильовий опір першого контура більший, ніж другого.Чим більший хвильовий (характеристичний) опір контура, тим менша сила струму в ньому за однакових інших умов

ЗАПИТАННЯ

1. Що можна вважати коливальним контуром?

2. Які фізичні величини є характеристиками (параметрами) коливального контура?
3. Які перетворення складових електромагнітної енергії спостерігаються в коливальному контурі?
4. Чому вільні коливання в контурі затухають?

5 Чи завжди в електричних колах, що мають індуктивність і ємність, можуть спостерігатись електромагнітні коливання?

6. Як встановлюються умови існування вільних електромагнітних коливань в електричних колах?
7. Що характеризує хвильовий опір?

Дата добавления: 2014-01-06