Кодирование по методу четности-нечетности

Контроль по четности, нечетности, по Хеммингу

Простым примером кода с обнаружением одной ошибки является код с битом чётности. Конструкция его такова: к исходному слову добавляется бит чётности. Если в исходном слове число единичек чётно, то значение этого бита 0 (для контроля нечетности - 1), если нечётно — 1 (для контроля нечетности - 0). Таким образом допустимые слова этого кода имеют чётное количество единичек. Если получено слово с нечётным (для контроля нечетности - четным) количеством единичек, то при передаче произошла ошибка.

При этом допускается, что может возникнуть только одна ошибка. В самом деле, для случая четности правильным будет только половина возможных комбинаций. Чтобы одна допустимая комбинация превратилась в другую, должно возникнуть, по крайней мере, два нарушения или четное число нарушений.

Таблица 3.1 Пример реализации метода четности

Число	Контрольный разряд	Проверка
		1-нарушение

Такое кодирование имеет минимальное кодовое расстояние, равное 2.

Можно представить и несколько видоизмененный способ контроля по методу четности – нечетности. Длинное число разбивается на группы. Контрольные разряды выделяются всем группам по строкам и по столбцам согласно следующей схеме:

Таблица 3.2 - Видоизмененный способ контроля по четности-нечетности

а 1	а 2	а 3	а 4	а 5	k1
а 6	a7	a8	a9	а10	k2
а11	а12	а13	а14	а15	K3
а16	а17	а18	а19	а20	k4
а21	а22	а23	а24	а25	k5
k6	k7	k8	k9	k10

Увеличение избыточности информации приводит к тому, что появляется возможность не только обнаружить ошибку, но и исправить её. В самом деле, пусть произошла неисправность в каком-то из разрядов этого числа (представим, что разряд а₁₈ изменил состояние, т.е. а₁₈=1). Это приводит к тому, что при проверке на четность сумма

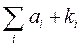
по соответствующим строкам изменится для значений, которые содержат элемент а₁₈, т.е. это будет четвертая сверху строка и третий слева столбец. Следовательно, нарушение четности по этой строке и столбцу можно зафиксировать, что в конечном счете означает обнаружение не только самой ошибки, но и места, где возникла ошибка. Изменив содержимое отмеченного разряда (в данном случае а₁₈) на противоположное, можно исправить ошибку.

Контроль по методу четности-нечетности широко используют в ЭВМ для контроля записи, считывания информации в запоминающих устройствах на магнитных носителях.

Пример. Определить и исправить ошибку в передаваемой информации вида:

Для контроля использовать метод четности по строкам и столбцам.

Решение. Прежде всего осуществим проверку на четность по каждой строке: k1 = 0; k2 = 1; k3 = 0; k4 = 0; k5 = 1.

Затем проверим на четность информацию по столбцам: k₆ = 0; k₇ = 1;

k₈ = 0; k₉ = 1; k₁₀ =0; k₁₁ =1; k₁₂=1.

Проверка показывает, что ошибка возникла в разряде второй строки и второго слева столбца. Следовательно, разряд, содержащий ошибочную информацию, находится на пере­сечении второй строки и второго столбца.

Ответ:

Дата добавления: 2014-01-06