Помехоустойчивость кода

Минимальное кодовое расстояние некоторого кода определяется как минимальное расстояние Хэмминга между любыми разрешенными кодовыми словами этого кода. У безызбыточного кода минимальное кодовое расстояние d_min=1. Чем больше минимальное кодовое расстояние, тем больше избыточность кода. Максимальное кодовое расстояние кода, очевидно, равно его размеру, т.е. числу двоичных разрядов в кодовом слове.

Очевидно, что 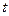-кратная ошибка приводит к тому, что искаженная кодовая комбинация отодвигается от исходной на расстояние 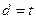. В то же время ошибка не может быть обнаружена, если она переводит одну разрешенную кодовую комбинацию в другую, тоже разрешенную. Следовательно, способность кода обнаруживать все ошибки некоторой кратности зависит от минимального расстояния между разрешенными кодовыми словами: чем больше минимальное кодовое расстояние, тем большей кратности требуется ошибка для перевода любой разрешенной кодовой комбинации в другую разрешенную. Код с минимальным кодовым расстоянием d_min способен обнаруживать любые ошибки кратностью

Способность кода исправлять обнаруженные ошибки состоит в возможности однозначного отнесения запрещенной кодовой комбинации к единственной разрешенной. Для этого необходимо, чтобы минимальное кодовое расстояние превышало расстояние, порождаемое действием двух любых ошибок. Действительно, в этом случае запрещенные кодовые комбинации, получающиеся в результате ошибок из одного кодового слова, никогда не совпадут с запрещенными комбинациями, получающимися в результате ошибок из любого другого кодового слова, а тем более – с другими разрешенными кодовыми словами. Таким образом, необходимо, чтобы выполнялось условие откуда следует

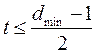
Рассмотрим n -разрядный код, основанный на n- кратном повторении каждого передаваемого символа. У него d_min= n. Следовательно, максимальная кратность обнаруживаемых ошибок равна n-1, что соответствует случаю искажения всех символов, кроме одного. Максимальная кратность исправляемых ошибок равна (n-1) /2, что соответствует искажению «почти» половины всех символов. Это соответствует фиксации ошибки при обнаружении хотя бы одного неодинакового символа и исправлению ошибки на основе определения, каких значений больше.

Рассмотрим n -разрядный код, основанный на введении одного разряда контроля четности. У него d_min= 2, и, следовательно, максимальная кратность обнаруживаемых ошибок равна 1, а исправляемых – 0 (код не способен исправлять ошибки).

Дата добавления: 2014-01-06