Цифровой метод контроля

Числовой метод контроля

При числовом методе контроля код заданного числа определяется как наименьший положительный остаток от деления числа на выбранный модуль р:

r_A = A-{A/p}p

где в фигурных скобках {} — целая часть от деления числа; А — контролируемое число.

Величина модуля р существенно влияет на качество контроля; если р = q (q — основание системы счисления, в которой выражено число) и имеет место числовой контроль, то контролируется только младший разряд числа и контроль как таковой не имеет смысла; для р = q^m справедливы аналогичные соображения, так как если m<n, то опять не все разряды числа участвуют в контроле и ошибки в разрядах старше m вообще не воспринимаются.

При числовом методе контроля по модулю p для определения остатка используют операцию деления, требующую больших затрат машинного времени. Для числового метода контроля справедливы основные свойства сравнений (сложение, умножение сравнений и т. д.). Поэтому, если А ≡ r_А(mod p);

В = rB(mod p), где 0≤rA≤p-1; 0≤rB≤p-1, то А + В = r_а + rB (mod p). Отсюда

r_A+B≡rA + rB(mod p)

Аналогичным образом доказывается справедливость и следующих соотношений:

r_A-B≡rA - rB(mod p);

r_AB≡rArB(mod p).

При цифровом методе контроля контрольный код числа образуется делением суммы цифр числа на выбранный модуль:

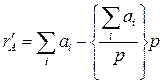
или

Возможны два пути получения контрольного кода: 1)непосредственное деление суммы цифр на модуль р; 2) суммирование цифр по модулю р.

Второй путь проще реализуется, так как если аi < р, то контрольный код получается только операцией суммирования.

Однако при цифровом методе свойства сравнений не всегда справедливы, и происходит это из-за наличия переносов (заемов) при выполнении арифметических действий над числами. Поэтому нахождение контрольного кода результата операции происходит обязательно с коррекцией.

Пусть заданы числа А и В и соответственно их контрольные коды

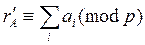; ; C = A + B.

Найдем контрольный код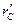

Видимо, когда есть результат операции, тогда найти 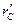методом суммирования цифр по модулю не сложно. Какова будет возможность получения 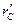через контрольные коды слагаемых ?

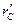Сумму цифр ci числа можно найти, зная цифры ai и bi и количество переносов в каждом разряде. Каждый перенос уносит из данного разряда q единиц и добавляет одну единицу в следующий разряд, т. е. сумма цифр уменьшится на величину q-1 на каждый перенос. Тогда

,

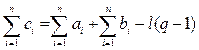где l — количество переносов, возникших при сложении.

Так как 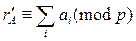; 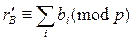, то .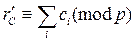

Подставив эти значения в предыдущую формулу, получим

.

Аналогичными рассуждениями можно показать, что для разности чисел

С = А - В

где s - количество заемов при выполнении операции.

Дата добавления: 2014-01-06