Контроль арифметических операций

Арифметические операции выполняют на сумматорах прямого, обратного и дополнительного кодов. Предположим, что изображение чисел (операнды) хранятся в машине в некотором коде, т. е. операция преобразования в заданный код или обратно проводится на выходе или входе машины. Методика реализации операций контроля представляется следующим образом.

Прежде всего, рассмотрим изображение числа в соответствующем коде как единую кодовую комбинацию, к которой можно приложить все сформулированные выше правила получения сверток. При этом требуется только обязательная кратность общего числа разрядов избранному модулю.

Рассмотрим последовательность действий на примере сумматора прямого кода.

Так как на сумматоре прямого кода складываются только цифровые части изображений чисел, а знак сохраняется, то контроль можно осуществить двумя способами:

1)раздельный контроль знаковой и цифровой частей изображений результата;

2)обобщенный контроль всего изображения.

При раздельном способе для контроля знаковых разрядов можно использовать средства для обнаружения переполнения, так как в случае модифицированного кода появление ошибок в знаковых разрядах приведет к несовпадению информации в них. При проверке правильности обработки цифровых частей изображений также не возникает особых трудностей.

При обобщенном способе контроля требуется коррекция контрольного кода результата из-за того, что знак результата при сложении повторяет знак слагаемых. Следовательно, можно констатировать, что контрольный код суммы чисел должен быть

,

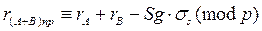где Sg — значение знакового разряда операндов; σ_s — вес старшего разряда свертки.

Обобщенный способ контроля может быть применен и для сумматоров обратного и дополнительного кодов.

При сложении чисел на сумматоре дополнительного кода потребуется коррекция контрольного кода в случае, если знаковые разряды изображений содержат единицу, так как при этом возникает единица переноса из знакового разряда. Очевидно, что контрольный код суммы будет равен

,

где α— коррекция (α = 1, если возник перенос из знакового разряда, и α = 0 — если переноса нет).

В случаях, когда операции преобразования в обратный или дополнительный код проводятся в процессе вычислений, целесообразна проверка этих преобразований.

Рассмотрим операцию преобразования из прямого кода в обратный.

Пусть [А]пр = аnаn-1...а1a0 — исходное число, представленное в прямом коде, для которого определяется остаток rA≡[А]пр(mod p). Подобные выражения можно записать для обратного кода rAоб≡[А]об(mod p) и инвертированного изображения .

Исходное число [А]_пр =а_n2ⁿ + А', где а_n — знаковый разряд; А —цифровая часть изображения.

Тогда

;

,

где 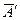— инвертированное изображение цифровой части числа

Левую часть равенства заменим сравнениями:

.

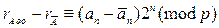Так как 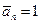, то 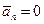, следовательно, .

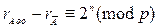Пусть 2n = k(mod p ). Тогда

Данное выражение дает возможность найти контрольное число для обратного кода при известных значениях величины р:

n…
p=3…
p=7…

Операцию преобразования в дополнительный код можно осуществить, используя соотношение между обратным и дополнительным кодами: дополнительный код отличается от обратного на единицу младшего разряда. Следовательно, контрольное число можно получить из выражения

Рассмотренную выше методику определения контрольных чисел для таких операций, как умножение или деление, можно применить для контроля работы ЭВМ, используя операционный контроль (контролем охватываются исходные числа и конечный результат) или шаговый контроль (проверяются все элементарные действия автомата при выполнении операции).

Дата добавления: 2014-01-06