Позиционные системы счисления

Совместимость преобразователей (взаимозаменяемость)

Большинство АЦП и ЦАП не являются универсально совместимыми по физическим, а некоторые и по электрическим параметрам. Физически корпуса различаются размерами, при этом наиболее распространенными размерами являются 2X2X0,4 дюйм (50,8Х Х50,8х0,16 мм) и 2X4X0,1 дюйм (50,8X101,6X2,54 мм). Часто выводы расположены не одинаково, поэтому потребитель должен проектировать свою печатную плату таким образом, чтобы она была пригодна для схем с различным расположением выводов, поставляемых разными фирмами-изготовителями. Одна из фирм изготовителей винит в этой несовместимости быстро изменяющееся и связанное с конкуренцией по габаритам производство преобразователей, которое вынуждает изменять конструкции изделий, что в свою очередь влечет за собой проблемы вторичных поставщиков.

Тем не менее, наблюдается некоторая тенденция в улучшении физической совместимости. Эта тенденция заключается в двухрядном расположении выводов и, в конечном счете, в появлении корпусов с двухрядным расположением выводов (как в случае с интегральными схемами преобразователей). Многие преобразователи могут быть приобретены по крайней мере у одной из вторичных фирм изготовителей.

С электрической точки зрения картина более благоприятная. Многие, хотя и не все, фирмы изготовители предусматривают одинаковые уровни выходных сигналов ЦАП и входных сигналов АЦП. К ним относятся общераспространенные значения выходных напряжений биполярных и однополярных ЦАП, равные 2,5; 5 и 10 В, и входных напряжений биполярных и однополярных АЦП, равные 5 и 10 В. Большинство преобразователей имеет источники питания ±15 В.

Система счисления - совокупность приемов и правил для записи чисел цифровыми знаками.

Наиболее известна десятичная система счисления, в которой для записи чисел используются цифры 0, 1, …, 9. Способов записи чисел цифровыми знаками существует бесчисленное множество.

Любая предназначенная для практического применения система счисления должна обеспечивать:

1. возможность представления любого числа в рассматриваемом диапазоне величин;
2. единственность представления (каждой комбинации символов должна соответствовать одна и только одна величина);
3. простоту оперирования числами;

В зависимости от способов изображения чисел цифрами, системы счисления делятся на непозиционные и позиционные.

Непозиционная система счисления – система, для которой значение символа не зависит от его положения в числе.

Для ее образования используют в основном операции сложения и вычитания. Например, система с одним символом-палочкой встречалась у многих народов. Для изображения какого-то числа в этой системе нужно записать количество палочек, равное данному числу. Эта система неэффективна, так как запись числа получается длинной. Другим примером непозиционной системы счисления является римская система, использующая набор следующих символов: I, V, X, L, C, D, M и т. д. В этой системе существует отклонение от правила независимости значения цифры от положения в числе. В числах LX и XL символ X принимает два различных значения: +10 – в первом случае и –10 – во втором случае.

Позиционная система счисления – система, в которой значение символа определяется его положением в числе: один и тот же знак принимает различное значение (арабская система счисления). Например, в десятичном числе 222 первая цифра справа означает 2, соседняя с ней – 20, а левая – 200.

Любая позиционная система характеризуется основанием. Основание (базис) позиционной системы счисления – количество знаков или символов, используемых для изображения числа в данной системе.

Позиционные системы счисления имеют ряд преимуществ перед непозиционными: удобство выполнения арифметических и логических операций, а также представление больших чисел, поэтому в цифровой технике применяются позиционные системы счисления.

Запись чисел может быть представлена в виде: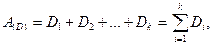

где:

A_(D) - запись числа A в системе счисления D;

D_i - символ системы, образующий базу.

По этому принципу построены непозиционные системы счисления.

В общем же случае системы счисления: A(B)=a₁B₁+a₂B₂ +...+a_nB_n.

Если положить, что B_i=q*B_i-1, а B₁=1, то получим позиционную систему счисления. При этом, если q=10, то мы имеем дело с привычной нам десятичной системой счисления.

На практике также используют другие позиционные системы счисления.

Таблица 7.1 – Различные используемые позиционные системы счисления

q	Название	Цифры
	двоичная	0, 1
	троичная	0, 1, 2
	восьмеричная	0,..., 7
	шестнадцатеричная	0,..., 9, A,..., F

Каждая система счисления имеет свои правила арифметики (таблица умножения, сложения). Поэтому, производя какие-либо операции над числами, надо помнить о системе счисления, в которой они представлены.

Если основание системы q превышает 10, то цифры, начиная с 10, при записи обозначают прописными буквами латинского алфавита: A,B,...,Z. При этом цифре 10 соответствует знак 'A', цифре 11 - знак 'B' и т.д.

В нижеследующей таблице приводятся десятичные числа от 0 до 15 и их эквивалент в различных системах счисления.

Таблица 7.2 – Различные эквиваленты десятичных чисел [0…15]

q=10	q=2	q=16	q=10	q=2	q=16
					A
					B
					C
					D
					E
					F

В позиционной системе счисления число можно представить через его цифры с помощью следующего многочлена относительно q:

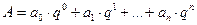
Вышеприведенное выражение формулирует правило для вычисления числа по его цифрам в q-ичной системе счисления. Для уменьшения количества вычислений пользуются так называемой схемой Горнера. Она получается поочередным выносом q за скобки:

результат вычисления многочлена будет всегда получен в той системе счисления, в которой будут представлены цифры и основание и по правилам которой будут выполнены операции.

Дата добавления: 2014-01-06