Табличный метод перевода

Перевод чисел делением на основание новой системы.

Перевод целых чисел осуществляется делением на основание q₂ новой системы счисления, правильных дробей – умножением на основание q₂. Действия деления и умножения выполняются по правилам q₁-арифметики. Перевод неправильных дробей осуществляется раздельно по указанным правилам, результат записывается в виде новой дроби в системе с основанием q₂.

Пример. Перевести десятичное число A = 61₁₀ в двоичную систему счисления (q = 2).

61 | 2

60 30 | 2

b₀ = 1 30 15 | 2

b₁ = 0 14 7 | 2

b₂ = 1 6 3 | 2

b₃ = 1 2 1 = b₅

b₄ = 1

Полученные остатки от деления записываем по порядку появления в ряд справа налево и таким образом получаем правильный ответ: 61₁₀ = 111101₂.

В простейшем виде табличный метод заключается в следующем: имеется таблица всех чисел одной системы с соответствующими эквивалентами из другой системы; задача перевода сводится к нахождению соответствующей строки таблицы и выбору из нее эквивалента. Такая таблица очень громоздка и требует большой емкости памяти для хранения.

Другой вид табличного метода заключается в том, что имеются таблицы эквивалентов в каждой системе только для цифр этих систем и степеней основания (положительных и отрицательных); задача перевода сводится к тому, что в выражение ряда для исходной системы счисления надо поставить эквиваленты из новой системы для всех цифр и степеней основания и произвести соответствующие действия (умножения и сложения) по правилам q₂-арифметики. полученный результат этих действий будет изображать число в новой системе счисления.

Пример. Перевести десятичное число A = 113₁₀ в двоичную систему счисления, используя таблицу эквивалентов цифр и степеней основания.

Таблица 7.3 – Таблица эквивалентов

Десятичное число	Двоичное число
	110 0100

Решение. Подставив значения двоичных эквивалентов десятичных цифр и степеней основания, получим:

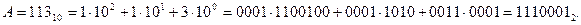
Ответ: 1110001₂.

На практике наиболее часто употребляются двоичная, десятичная и шестнадцатеричная системы счисления. Приведем для них правила взаимного перевода:

Правила перевода целых чисел (результат – целое число):

Из десятичной системы счисления в двоичную и шестнадцатеричную:

1. исходное целое число делится на основание системы счисления, в которую переводится (2 или 16); получается частное и остаток;
2. если полученное частное не делится на основание системы счисления так, чтобы образовалась целая часть, отличная от нуля, процесс умножения прекращается, переходят к шагу 3. Иначе над частным выполняют действия, описанные в шаге 1;
3. все полученные остатки и последнее частное преобразуются в соответствии с таблицей в цифры той системы счисления, в которую выполняется перевод;
4. формируется результирующее число: его старший разряд - полученное последнее частное, каждый последующий младший разряд образуется из полученных остатков от деления, начиная с последнего и кончая первым.

Рисунок 8.1 – Перевод числа 19 в двоичную систему счисления

Рисунок 8.2 – Перевод числа 19 в шестнадцатеричную систему счисления

Рисунок 8.3 – Перевод числа 123 в шестнадцатеричную систему счисления

Из двоичной и шестнадцатеричной систем счисления в десятичную:

В этом случае рассчитывается полное значение числа по формуле.

Пример. Выполнить перевод числа 13₁₆ в десятичную систему счисления.

Имеем: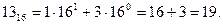

Таким образом, 13₁₆ = 19.

Пример. Выполнить перевод числа 10011₂ в десятичную систему счисления.

Имеем: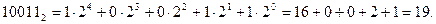

Таким образом, 10011₂ = 19.

Из двоичной системы счисления в шестнадцатеричную:

1. исходное число разбивается на тетрады (т.е. 4 цифры), начиная с младших разрядов. Если количество цифр исходного двоичного числа не кратно 4, оно дополняется слева незначащими нулями до достижения кратности 4;
2. каждая тетрада заменятся соответствующей шестнадцатеричной цифрой в соответствии с Таблица 7.2.

Пример. Выполнить перевод числа 10011₂ в шестнадцатеричную систему счисления.

Поскольку в исходном двоичном числе количество цифр не кратно 4, дополняем его слева незначащими нулями до достижения кратности 4.

Имеем:

Рисунок 8.4 – Перевод числа 10011₂ в шестнадцатеричную систему счисления

В соответствии с Таблица 7.2:

0011₂ = 11₂ = 3₁₆

0001₂ = 1₂ = 1₁₆.

Тогда 10011₂ = 13₁₆.

Из шестнадцатеричной системы счисления в двоичную:

1. каждая цифра исходного числа заменяется тетрадой двоичных цифр в соответствии с Таблица 7.2. Если в Таблица 7.2 двоичное число имеет менее 4 цифр, оно дополняется слева незначащими нулями до тетрады;
2. незначащие нули в результирующем числе отбрасываются.

Пример. Выполнить перевод числа 13₁₆ в двоичную систему счисления.

Согласно Таблица 7.2 имеем:

1₁₆ = 1₂ и после дополнения незначащими нулями 1₂ = 0001₂;

3₁₆ = 11₂ и после дополнения незначащими нулями 11₂ = 0011₂.

Тогда 13₁₆ = 00010011₂.

Удаляем незначащие нули - 13₁₆ = 10011₂.

Правила перевода правильных дробей (результат – правильная дробь):

Из десятичной системы счисления в двоичную и шестнадцатеричную:

1. исходная дробь умножается на основание системы счисления, в которую переводится (2 или 16);
2. в полученном произведении целая часть преобразуется в соответствии с таблицей в цифру нужной системы счисления и отбрасывается - она является старшей цифрой получаемой дроби;
3. оставшаяся дробная часть вновь умножается на нужное основание системы счисления с последующей обработкой полученного произведения в соответствии с шагами 1 и 2;
4. процедура умножения продолжается до тех пор, пока ни будет получен нулевой результат в дробной части произведения или ни будет достигнуто требуемое количество цифр в результате;
5. формируется результат: последовательно отброшенные в шаге 2 цифры составляют дробную часть результата, причем в порядке уменьшения старшинства.

Пример. Выполнить перевод числа 0,847 в двоичную систему счисления. Перевод выполнить до четырех значащих цифр после запятой.

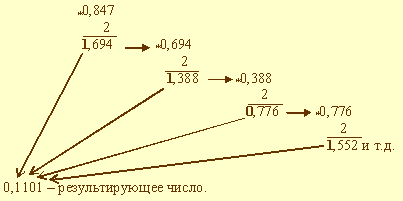
Рисунок 8.5 – Перевод числа 0,847 в двоичную систему счисления

В данном примере процедура перевода прервана на четвертом шаге, поскольку получено требуемое число разрядов результата. Очевидно, это привело к потере ряда цифр.

Ответ 0,847 = 0,1101₂.

Пример. Выполнить перевод числа 0,847 в шестнадцатеричную систему счисления. Перевод выполнить до трех значащих цифр.

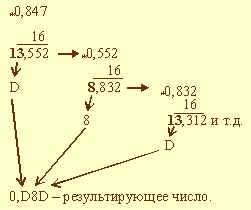
Рисунок 8.6 – Перевод числа 0,847 в шестнадцатеричную систему счисления

В данном примере также процедура перевода прервана.

Ответ 0,847 = 0,D8D₂.

Из двоичной и шестнадцатеричной систем счисления в десятичную:

В этом случае рассчитывается полное значение числа по формуле, причем коэффициенты a_i принимают десятичное значение в соответствии с таблицей.

Пример. Выполнить перевод из двоичной системы счисления в десятичную числа 0,1101₂.

Имеем: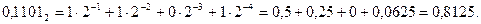

Расхождение полученного результата с исходным для получения двоичной дроби числом вызвано тем, что процедура перевода в двоичную дробь была прервана.

Ответ 0,1101₂ = 0,8125.

Пример. Выполнить перевод из шестнадцатеричной системы счисления в десятичную числа 0,D8D₁₆.

Имеем:

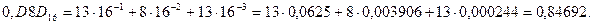
Расхождение полученного результата с исходным для получения двоичной дроби числом вызвано тем, что процедура перевода в шестнадцатеричную дробь была прервана.

Ответ 0,D8D₁₆ = 0,84692.

Из двоичной системы счисления в шестнадцатеричную:

1. исходная дробь делится на тетрады, начиная с позиции десятичной точки вправо. Если количество цифр дробной части исходного двоичного числа не кратно 4, оно дополняется справа незначащими нулями до достижения кратности 4;
2. каждая тетрада заменяется шестнадцатеричной цифрой в соответствии с таблицей.

Пример. Выполнить перевод из двоичной системы счисления в шестнадцатеричную числа 0,1101₂.

Имеем: 0,1101₂ = 0,1101₂ (дробь делится на тетрады).

В соответствии с Таблица 7.2 1101₂ = D₁₆.

Тогда имеем 0,1101₂ = 0,D₁₆.

Пример. Выполнить перевод из двоичной системы счисления в шестнадцатеричную числа 0,0010101₂.

Добавим справа незначащий ноль: 0,0010101₂ = 0,00101010₂.

В соответствии с Таблица 7.2 0010₂ = 10₂ = 2₁₆ и 1010₂ = A₁₆.

Тогда имеем 0,0010101₂ = 0,2A₁₆.

Из шестнадцатеричной системы счисления в двоичную:

1. каждая цифра исходной дроби заменяется тетрадой двоичных цифр в соответствии с Таблица 7.2;
2. незначащие нули отбрасываются.

Пример. Выполнить перевод из шестнадцатеричной системы счисления в двоичную числа 0,2А₁₆.

Согласно Таблица 7.2 имеем 2₁₆ = 0010₂ и А₁₆ = 1010₂.

Тогда 0,2А₁₆ = 0,00101010₂.

Удаляем незначащие нули и получаем ответ: 0,2А₁₆ = 0,0010101₂.

Правило перевода дробных чисел:

Отдельно переводится целая часть числа, отдельно - дробная. Результаты складываются.

Пример. Выполнить перевод из десятичной системы счисления в шестнадцатеричную числа 19,847. Перевод выполнять до трех значащих цифр после запятой.

Представим исходное число как сумму целого числа и правильной дроби:

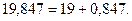
Из рассматриваемых выше примеров следует:

19 = 13₁₆;

0,847 = 0,D8D₁₆.

Тогда имеем: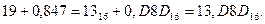

Ответ 19,847 = 13,D8D₁₆.

Дата добавления: 2014-01-06