Нормативные и расчетные сопротивления

Основы расчета деревянных конструкций

Расчет ДК в Украине производится по методу предельных состояний. Предельными называются такие состояния, при которых ДК перестают удовлетворять требованиям эксплуатации. Различают две группы предельных состояний: 1) по несущей способности (прочности, устойчивости) и 2) по деформациям (прогибам, перемещениям). Требования расчета по предельным состояниям заключается в том, чтобы было соблюдено условие неразрушимости. Исходя из этого принципа, усилия или напряжения, деформации и перемещения от учитывающих нагрузок и воздействий не превышая предельных значений, устанавливаемых нормами проектирования. Расчет по первому предельному состоянию производится на расчетные нагрузки, по второму – на нормативные. Аналитически первая группа предельных состояний представляет N≤Ф. N – максимально возможное усилие за весь период эксплуатации, Ф – предельная несущая способность.

Для 2 группы – δ_ф≤[δ], δ_ф – фактическая деформация, [δ] – нормируемая деформация.

Преимущества методики по предельным состояниям заключается в том, что она позволяет дифференцированно оценить влияние на несущую способность изменчивость внешних нагрузок (коэффициент нагрузки n), изменчивость механических свойств материала (коэффициент безопасности по материалам k), условия работы конструкций (коэффициент условий работы m) и оценить надежность конструкции (коэффициент надежности K_н)

В зависимости от продолжительности действия нагрузки следует различать постоянные и временные (длительные, кратковременные, особые) нагрузки.

Расчет конструкций по предельным состояниям следует выполнять с учётом наиболее неблагоприятных сочетаний нагрузок.

При количестве нагрузок более двух, учитывается коэффициент сочетаний, приведенных в СНиП 2.01.07_85 “ Загрузки и воздействия ”

Основной характеристикой сопротивления материала силовому воздействию служит нормативное сопротивление. За R^н принимается вероятное значение предельной прочности.

Расчетное сопротивление определяется по формуле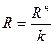

где k – коэффициент безопасности по материалу

Коэффициент безопасности по материалу k учитывает длительность нагрузки, наличие пороков древесины (сучки, косослой), переходы от малых стандартных образцов к элементам строительных размеров.

Этот коэффициент равен при растяжении вдоль волокон 5,5, при сжатии вдоль волокон 2,2, при поперечном изгибе 3,8. Расчетные сопротивления для сосны, ели приведены в СНиП II – 25 – 80, для других пород вводится коэффициент m_П.

Расчетное сопротивление древесины местному смятию поперек волокон на части длины

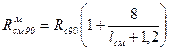
где R_{c 90} – расчетное сопротивление сжатию и смятию по всей поверхности поперек волокон

l_см – длина площадки смятия в см.

Расчетное сопротивление древесины смятию под углом α к направлению волокон определяется

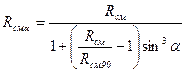
Расчетное сопротивление древесины скалыванию под углом к направлению волокон

Нагрузки и воздействия

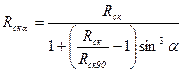
Влияние на д. k температуры, влажности, агрессивности среды и пр. учитывается коэффициентом условий работы материалов m, на который в необходимых случаях умножаются расчетные сопротивления.

m_В – учитывает различные условия эксплуатации. m_В≤1

m_Н – учитывается для конструкций подвергаемых на воздействие кратковременных нагрузок (ветровая, монтажная, сейсмическая от тяжения проводов)

m_Н>1 (1,2÷1,6); 2,2

Для изгибаемых, внецентр. сжатых, сжато - изг. клееных элементов с h_сеч>50 см значения R_и и R_с умножают на коэффициент m_б

чем больше высота сечения тем меньше m_б (от 1 до 0,8)

Расчет деревянных конструкций цельного сечения

1. Центральное растяжение. Деревянные элементы, работающие на центр. растяжение, рассчитывают по наиболее ослабленному сечению.

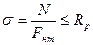· m o

При определении F_нт ослабления расположенные на участке длиной до 200 мм, следует принимать совмещенными в одном сечении. Коэффициент m_o=0,8, учитывая концентрацию напряжения в местном ослаблении.

2.Центральное сжатие. Расчет деревянных конструкций на центральном сжатие производят на прочность и устойчивость. Расчет на прочность необходим для коротких длина < 7 δ, где δ - размер поперечного сечения.

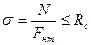
на устойчивость

Сжатые стержни, имеющие большую длину и не закрепленную в поперечном направлении помимо расчета на прочность рассчитываются на продольный изгиб. Явление продольного изгиба, как известно, закл. в том, что гибкий центрально – сжатый прямой стержень теряет устойчивость и начинает выпучиваться при напряжениях, значительно меньших предела прочности.

Теоретическое значение критической силы или критического напряжения для абсолютно упругого стержня определяется по формуле Эйлера (1757 г.)

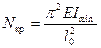; Разделив на F получим критическое напряжение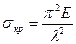

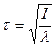
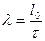
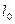- расчетная длина стержня,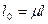

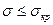
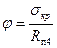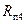; - предел прочности

Опыты показывают, что отношение E/R_пу довольно постоянно как при кратковременном, та при длительном действии нагрузки и приближенно ≈ 312

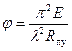Тогда 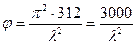(уравнение гиперболы Эйлера)

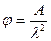
Формула справедлива при критическом напряжении меньше предела пропорциональности при λ>70

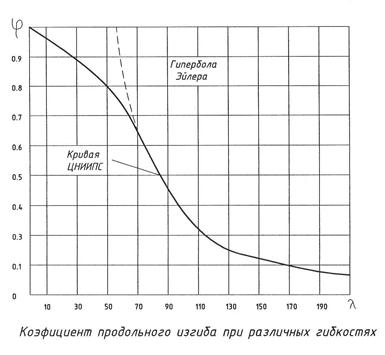
Для дерева кривая φ за пределом упругости, φ определяется по формуле

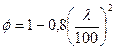(λ≤70) а=1

А=3000

А=2500 (фанера)

А=1097 (полиэфир, стеклопластик)

А=580 (оргстекло)

Гибкость элементов цельного сечения определяется по формуле

,

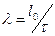Величина гибкости может быть также ограничена, из-за чрезмерного

Провисания стержня.

Предельные гибкости:

[λ]=120 – сжатые пояса, опорные раскосы и опорные стойки ферм, колонны

[λ]=150 остальные элементы ферм и др. сквозные конструкции, растянутые пояса ферм в вертикальной плоскости.

[λ]=200 для связей

Расчетная площадь: 1) при отсутствии ослаблений F_расч=F_δр

2) при наличии ослаблений не выходящих на кромки, если F_осл > 25% F_δр→ F_расч=4/3 F_нт

3) При наличии симметрических ослаблений F_расч=F_нт

Поперечный изгиб

Расчет на поперечный изгиб заключается в проверке прочности и жесткости.

На прочность 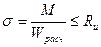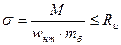; где коэффициент учитывет размеры сечения

Расчет производится в месте возникновения мах момента и в месте мах ослаблений; Для цельных элементов W_расч=W_нт, где W_нт – момент сопротивления нетто; причем ослабления расположение на участке 20 см, принимается совмещенным в одном сечении.

Для изгибаемых элементов на податливых связях расчетный момент сопротивления следует принимать

Wрасч=W_нт·k_w

k_w приведены в Снип II-35-80 табл. 13

Помимо этой проверки, необходимо проверить на прочность по скалыванию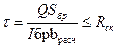

Расчет ДК на изгиб по нормальным напряжениям производят приближенно. При более точном методе потребовался бы учет различных модулей упругости в сжатой и растянутой зонах.

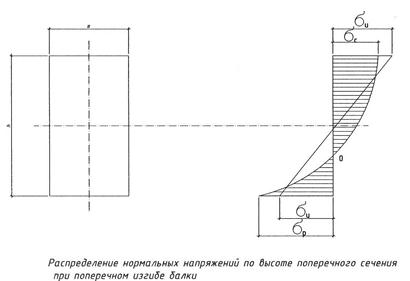
Из этого рисунка видно, что в сжатой зоне развиваются большие пластические деформации, которые нарушают прямолинейность эпюры нормативного напряжения. Т.о нормальное напряжение определяют при двух допущениях

1) что Е_с=Е_р

2) распределение 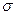по высоте прямолинейно

Расчет изгибаемых элементов по второму предельному состоянии на жесткость заключается в определении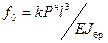

При учете влияния касательных напряжений на прогиб он определяется по формуле f 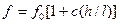, где f о – прогиб без учета деформаций сдвига и с – коэффициент учитывающий форму сечения балки и расчетную схему.

Косой изгиб

Этот изгиб, при котором направление действия усилия не совпадает с направлением одной из главных осей поперечного сечения элемента.

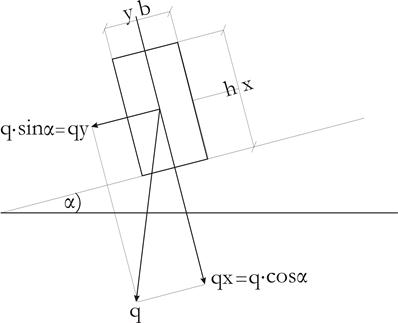
В этом случае действующее усилие раскладывается по направлению главных осей сечения, затем определяются изгибающие моменты, действующих в этих плоскостях. Нормальные напряжения опр. По формуле

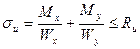
Полный прогиб равен геометрической сумме прогибов от усилий

qx и qу

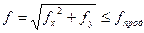
Дата добавления: 2014-01-06