Метод последовательных интервалов

Метод последовательных интервалов применяется для исследования динамической устойчивости электрических систем. Этот простой метод интегрирования дифференциальных уравнений позволяет получить удовлетворительную точность решения, если диапазон интегрирования не превышает 1-2 с.

Пусть необходимо проинтегрировать дифференциальное уравнение движения ротора генератора:

где - постоянная инерции агрегата;

e - угловое ускорение ротора генератора;

DP - избыточная мощность на валу генератора.

DP = P_т – P_э ,

где Р_т - мощность турбины;

P_э – мощность генератора.

Уравнения движения ротора нелинейно и не может быть решено в общем виде. В практике инженерных расчетов часто пользуются упрощенными методами. Одним из них является метод последовательных интервалов.

В соответствии с этим методом весь процесс качания ротора генератора разбивается на ряд интервалов времени Dt и для каждого из них последовательно вы-

числяется приращение угла Dd.

Выбирая одинаковые интервалы во времени, очевидно, будем иметь неодинаковые интервалы по углу.

Каждый интервал характеризуется некоторым значениями начальных и конечных величин угла, скорости и ускорения. Начальные значения этих величин в последующих интервалах равны конечным в предыдущих интервалах. Для упрощения расчетов в пределах каждого интервала угловое ускорение e_i считается постоянным и равным его значению в начале данного интервала.

Интервал Dt выбирается в пределах 0,02 – 0,1 с в зависимости от применяемых вычислительных средств и целей расчета. Наиболее точные результаты, разумеется, получаются при меньших интервалах, но при этом возрастает длительность расчетов. Поэтому при расчетах с помощью калькуляторов обычно принимают величину интервала Dt = 0,5 с.

В первом интервале начальное значение Dw₍₀₎ = 0,

где Dw - относительная угловая частота.

Dw = w - w₀,

где w - угловая частота ротора;

w₀ - синхронная угловая частота.

Так как Dw₍₀₎ = 0, то при постоянном угловом ускорении, равном e ₍₀₎, в первом интервале изменение угла между осями магнитных полей ротора и статора будет происходить по закону равноускоренного движения:

Dd₍₁₎ = 0,5 × e₍₀₎ × Dt² . (65)

Значение e_{(0 )} определяется по формуле

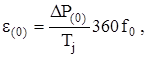
где DP₍₀₎ - избыточная мощность в момент времени t =0, о.е.;

f₀ - частота, Гц.

Во втором интервале приращение угла составит

Dd₍₂₎ = Dw₍₁₎×Dt + 0,5 e₍₁₎×Dt², (66)

где e₍₁₎ - угловое ускорение, обусловленное избыточной мощностью DP₍₁₎ ;

Dw₍₁₎ - относительная угловая частота в конце первого интервала.

Значение относительной угловой частоты в течение первого интервала времени непостоянно.

Определим значение Dw₍₁₎ по среднему угловому ускорению:

Dw₍₁₎=0,5(e₍₀₎ + e ₍₁₎ )Dt.

Подставив это значение в уравнение (66), будем иметь

Dd₍₂₎ = 0,5 e ₍₀₎×Dt² + e ₍₁₎×Dt²,

или с учетом соотношения (65)

Dd₍₂₎ = Dd₍₁₎ + e ₍₁₎×Dt².

Аналогично можно получить выражения для приращения угла в третьем, четвертом и любом последующем интервале.

Выражая время в секундах, а углы – в электрических градусах, будем иметь

Dd₍₁₎ = 0,5×К× DP₍₀₎;

Dd₍₂₎ = Dd₍₁₎+ К× DP₍₁₎;

Dd₍₃₎ = Dd₍₂₎+ К× DP₍₂₎;

Dd_(n) = Dd_{(n -1)}+ К× DP_{(n -1)},

где (67)

Как следует из выражения (67) коэффициент К представляет собой произведение всех постоянных численного интегрирования.

5 ПРИМЕНЕНИЕ ТЕОРИИ ВЕРОЯТНОСТЕЙ В ЭЛЕКТРОЭНЕРГЕТИКЕ

Дата добавления: 2014-01-06