Статистические численные характеристики случайных величин

Наиболее важными характеристиками случайной величины являются математическое ожидание, дисперсия и среднее квадратическое отклонение (называемое также стандартным отклонением или стандартом).

Перечисленные характеристики относятся к генеральной совокупности. Экспериментально полученные массивы чисел представляют собой случайную выборку, лишь приближенно характеризующую генеральную совокупность и, тем более, теоретическое распределение.

Поэтому при обработке данных наблюдений или эксперимента следует говорить не о параметрах распределения, а об оценках этих параметров или, что то же самое, о статистических параметрах.

Статистические параметры обычно обозначают звездочкой. Так, если математическое ожидание, дисперсия и стандартное отклонение случайной величины X были обозначены m_x, D_x, s_x, то для соответствующих величин, полученных опытным путем, используются обозначения m_x^*, D_x*, s_x^*. Оценку стандартного отклонение обозначают также буквой s.

Выборочная характеристика, используемая в качестве приближенного значения неизвестной генеральной характеристики, называется ее точечной статистической оценкой. Наряду с точечными применяются также интервальные оценки.

В ряде литературных источников термин «оценка» опускается. Однако расчеты производятся по формулам, применимым к статистическим характеристикам.

Оценкой математического ожидания случайной величины является среднее арифметическое её наблюдаемых значений.

Оценка дисперсии (которая называется также выборочной дисперсией или дисперсией выборки) вычисляется по формуле

Оценка стандартного отклонения находится по формуле

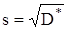
Дата добавления: 2014-01-06