Представление сигналов во временной области

Измерительный сигнал во временной области рассматривается как функция времени, характеристики которой содержат информацию, заключенную в сигнале.

Рассмотрим некоторые наиболее типичные сигналы.

Гармонические сигналы (рис. 5):

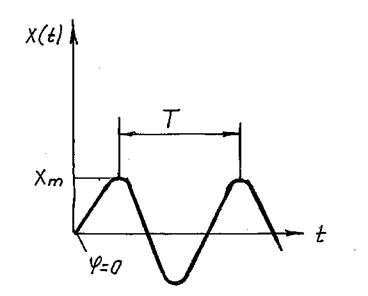
Рис. 5. Пример гармонического сигнала

()

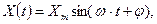где X_m, w, j - параметры, которые могут быть информативными;

X_m- амплитуда;

w- частота;

j- фаза.

. ()

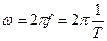В случае модуляции синусоидальный сигнал может быть либо информативным, либо несущим.

Периодические сигналы (рис. 6):

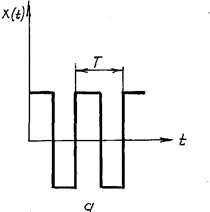
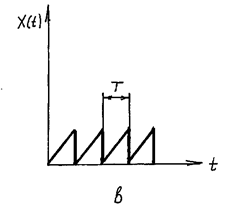
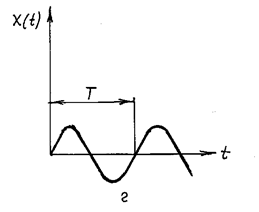
Рис. 6. Примеры периодических сигналов

где -µ < t < µ;

Т- период сигнала;

n=1,2,….

Периодический сигнал может быть представлен с помощью ряда Фурье:

()

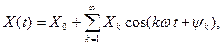В этом случае параметры X_k и y_k могут быть информативными.

Пример: вибродиагностика машин и механизмов. Гармоники вибросигнала несут в себе информацию о различных деталях и повреждениях машин.

Почти периодические сигналы:

Состоят из конечного числа периодических составляющих и характеризуются отсутствием кратного периода:

()

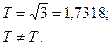
Импульсные сигналы (рис.7):

Имеют отличную от нуля энергию только в определенном интервале времени.

.

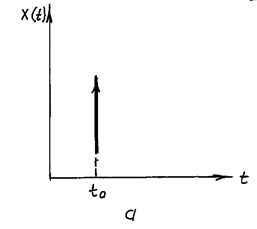
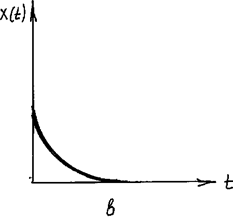
Рис. 7. Примеры импульсных сигналов: а – единичный импульс (функция Дирака) 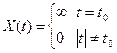; б – прямоугольный импульс 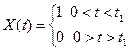; в – экспоненциальный импульс

В качестве информативных параметров может выступать амплитуда или максимальное значение импульса, длительность импульса, период повторения, крутизна переднего или заднего фронтов, площадь под кривой, энергия импульса.

Площадь импульса можно определить по следующему выражению:

()

Энергия импульса:

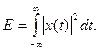
Случайные процессы и сигналы. Классификация, свойства, параметры

Случайные процессы классифицируются и обрабатываются в соответствии с теорией случайных процессов (ТСП).

ТСП– математическая наука, изучающая закономерности случайных явлений в динамике их развития. ТСП иногда называют теорией случайных функций.

При изучении окружающего мира мы постоянно сталкиваемся с процессами, явлениями, течение которых заранее предсказать в точности невозможно. Это обстоятельство вызвано влиянием случайных факторов, воздействующих на ход процесса.

Например, напряжение в электросети, амплитуда которого должна быть постоянна, фактически меняется во времени, то есть, колеблется вокруг номинального значения под влиянием таких факторов, как количество и вид включенных в сеть электроприборов, моменты их включения и выключения, природные возмущения и т.д.

В природе нет совершенно неслучайных процессов (в точности детерминированных), но есть процессы, на ход которых случайные факторы влияют так слабо, что ими можно пренебречь. В тоже время есть множество процессов, где случайность играет основную роль (броуновское движение). Это две крайности. В измерительной технике мы работаем с целым спектром процессов, лежащим между указанными границами, в которых случайность играет большую или меньшую роль.

Случайный процесс в любой физической системе S представляет собой случайные переходы системы из состояния в состояние. Общее состояние системы может быть охарактеризовано с помощью численных переменных (в простейшем случае– одной, в более сложных– множеством).

В рассмотренном примере с напряжением электросети, процесс описывается одной переменной (напряжением U). Если рассмотреть изменение напряжения во времени, то следует оперировать понятием случайной функции времени U(t). Здесь, при t=const случайная функция обращается в случайную величину U_t.

В результате опыта или измерительного эксперимента случайная функция превращается в обычную неслучайную функцию. Например, если в ходе времени непрерывно измерять напряжение в сети, получится неслучайная функция U(t), флуктуирующая вокруг номинала U₀ (рис. 8).

Рис. 8. Пример неслучайной функции

Случайный сигнал можно определить как семейство случайных переменных 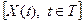, которые зависят от параметра t, принадлежащего соответствующему множеству Т. В этом случае параметр t имеет смысл времени.

При Т={0<t£µ} или {-µ<t<µ} случайную функцию рассматривают как ансамбль выборочных функций, а при конечном интервале времени– как ансамбль реализаций (рис. 9).

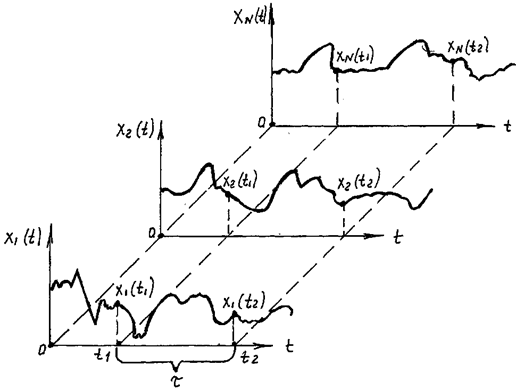
X(t) – случайная функция;

X_j(t) – реализация (где j=1, 2,..., ¥)

Рис. 9. Пример ансамбля реализаций

Учитывая обозначения, случайный сигнал, описываемый случайной функцией X(t), есть ансамбль реализаций X₁(t), X₂(t),…,X_n(t),…,X_µ(t). Значение случайной функции X(t) при фиксированном значении аргумента X(t_j)=X_j являются случайными величинами. При неизменных условиях протекания случайного процесса значения X(t₁)=X₁ в реализациях X_j(t₁), полученных для идеальных устройств, будут различными.

Любое конкретное значение X_j случайной величины X называют выборочным.

Случайный сигнал, состоящий из смеси полезного сигнала S(t) и шума n(t) (X(t)=F[S(t), n(t)]) сопоставляется с термином случайного процесса.

В теоретических исследованиях ансамбль выборочных функций (реализаций) принимается бесконечным (N®µ).

Если N¹µ (ансамбль конечный), то результат определения значения вероятностной характеристики G(X) по ограниченной совокупности выборочных называется оценкой G^*(X) или .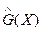

Случайные сигналы делят на стационарные и нестационарные. Случайный сигнал называется стационарным, если он описывается стационарной случайной функцией. Случайная функция называется стационарной в некотором смысле, если ее определенная группа вероятностных характеристик инвариантна во времени, то есть не изменяется при замене аргумента t на t+t для всех t, таких, что t_jÎT; (t_j+t)ÎT.

В теории измерений часто используют следующее определение стационарности: стационарным называется сигнал, в котором в любом сечении времени закон распределения величины и характеризующие его моменты остаются неизменными (рис. 10).

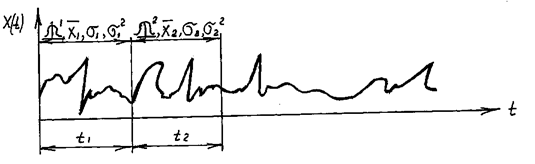
Закон распределения P(x)₁=P(x)₂;

среднее ;

СКО ;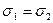

дисперсия .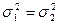

Рис. 10. Пример стационарного сигнала

Такое определение стационарности является несколько обобщенным.

Стационарные случайные функции, следовательно, и сигналы делят на стационарные в узком смысле (строго стационарные) и широком смысле (слабо стационарные или стационарные второго порядка).

Кроме этого, случайные сигналы делят на: стационарные эргодические и стационарные неэргодические; на непрерывные и дискретные; на широкополосные и узкополосные.

Случайный сигнал называется стационарным в узком смысле, если все конечномерные функции распределения вероятностей любого порядка инвариантны относительно сдвига во времени, то есть при любых N и t выполняется равенство:

F_N(X₁,t₁; X₂,t₂; …; X_N,t_N)= F_N(X₁,t₁+t; X₂,t₂+t; …; X_N,t_N+t).

Случайный сигнал {X(t), tÎT} называется стационарным в широком смысле, если:

1) он определен на интервале [-µ; µ];

2) его математическое ожидание определено и одинаково для всех tÎ[-µ; µ];

3) корреляционная функция определена для всех t₁,t₂Î[-µ; µ] и не изменяется при замене t₁,t₂ на t₁+t₀, t₂+t₀, и зависит лишь от разности времен t₂-t₁=t;

4) его дисперсия определена и одинакова для всех tÎ[-µ; µ].

Строго стационарные сигналы образуют отдельный подкласс в классе стационарных. Они стационарны в широком смысле, но не наоборот.

Пример стационарного в широком смысле случайного сигнала:

X(t)=A(t)×cos(w₀×t+j),

где j - случайная величина, равномерно распределенная в интервале -p£j£p;

A(t)- независящий от j стационарный в широком смысле случайный сигнал.

При теоретическом определении статистических характеристик случайных функций обычно оперируют с ансамблем. При проведении реальных измерений за ограниченный промежуток времени можно получить лишь одну реализацию случайного сигнала и, следовательно, усреднение возможно по времени в пределах одной реализации.

Стационарные случайные сигналы, для которых результаты усреднения па ансамблю и по времени совпадают, называются стационарными, эргодическими. При этом речь идет о предельных значениях статистических характеристик, то есть:

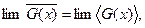
где 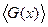- статистическая характеристика случайного сигнала X(t), определяемая усреднением по N реализациям;

- статистическая характеристика случайного сигнала X(t), полученная путем усреднения во времени Т (рис. 11).

Рис. 11. Усреднение по ансамблю и реализации

Существует еще одно определение эргодичности. Стационарный случайный процесс X(t) обладает эргодическими свойствами математического ожидания, то есть:

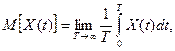
если и только если выполняется равенство:

()

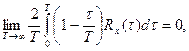где R_x(t)- корреляционная функция процесса X(t).

Стационарный случайный процесс X(t) считается эргодическим относительно корреляционной функции R_x(t):

если и только если выполняется равенство:

где R_x(t’)- корреляционная функция процесса X(t+t)X(t).

Стационарные случайные сигналы, для которых не выполняется условие 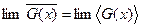, являются неэргодическими случайными сигналами.

Сигнал 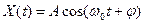, где А- амплитуда и j- начальная фаза, распределенная равномерно в интервале -p£j£p,– независимые случайные величины, является эргодичным, так как корреляционная функция R_x(t), рассчитанная усреднением по ансамблю и равная:

,

не совпадает с корреляционной функцией, рассчитанной усреднением по времени и равной:

,

где А_j- одно из возможных значений, принятое случайной величиной А в j-й реализации.

В качестве примера на рис. 12 изображен эргодический стационарный процесс, в котором математическое ожидание, полученное усреднением по ансамблю m_xT, совпадает с математическим ожиданием, полученным усреднением по времени m_xk, то есть m_xk=m_xT=0.

Рис. 12. Эргодический стационарный случайный процесс

На рис. 13 изображен неэргодический стационарный процесс.

Рис. 13. Неэргодический стационарный случайный процесс

В этом процессе m_xk¹m_xT. Математическое ожидание найденное для процесса (рис. 13) путем усреднения по ансамблю, даст текущее математическое ожидание.

Существуют понятия «локальной стационарности» и «локальной эргодичности». Они описывают свойства случайного процесса, проявляющиеся на конечном объеме выборок.

Дата добавления: 2014-01-06