Спектральное представление периодических сигналов

Периодический сигнал с периодом Т, который описывается некоторой функцией у(х), отвечающей условиям Дирихле, можно представить в виде ряда Фурье:

,

где а₀/2- постоянная составляющая;

a_k, b_k- коэффициенты ряда Фурье.

Коэффициенты определяются для абсолютно интегрируемой на отрезке [-p; p] функции у(х) по формулам Эйлера-Фурье:

;

.

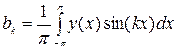В приведенных выражениях х может иметь размерность времени(t).

Часто, особенно в радиотехнических расчетах, периодические сигналы представляются как функции времени y(t) на отрезке [0, T] с периодом Т=1/f₁, где f₁-частота первой гармоники периодического сигнала. В этом случае ряд Фурье представляется в виде:

,

где ;

.

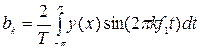В этом случае коэффициенты a_k и b_k описывают косинусную и синусную составляющие k-ой гармоники сигнала с периодом Т и частотой f₁=1/T.

Часто используется иная форма ряда Фурье (особенно при синтезе различных сигналов):

,

или при использовании общепринятых обозначений:

,

где 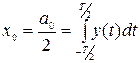- постоянная составляющая сигнала;

x_k=A_k- амплитуда k-й гармоники;

k- номер гармоники;

;

- частота k-й гармоники;

j_k- фаза k-й гармоники.

Как видно из выражений, периодический сигнал y(t) представляется как сумма бесконечно большого числа гармонических составляющих с амплитудами x_k, частотами f_k и фазами j_k.

Разложение функции на гармонические составляющие, то есть вычисление коэффициентов Фурье, называется гармоническим или спектральным анализом. Воссоздание функции, представленной рядом Фурье, называют спектральным синтезом.

Гармонику с k=1 называют основной или первой гармоникой сигнала. Она задает его частоту повторения f₁. Остальные гармоники называют высшими из частных. Они определяются как f_k=k×f₁, k=2, 3, 4, …

Таким образом, спектр периодических сигналов, представимых рядом Фурье, дискретный, то есть он содержит набор фиксированных частот f_k, где k=1, 2, 3,…. Для непериодических сигналов спектр будет сплошным.

Определение: совокупность величин x_k есть спектр амплитуд, совокупность величин j_k- спектр фаз.

При анализе реальных процессов x_k можно определить как:

.

На рис. 37 представлены примеры некоторых периодических сигналов и их спектров.

Рис. 37. Примеры некоторых периодических сигналов и их спектров: а – для гармонического процесса; б – для полигармонического процесса (сумма 4-х синусоид)

Для анализа дискретных сигналов в частотной области используют дискретное преобразование Фурье.

При дискретизации времени непрерывный сигнал x(t) преобразуется в последовательность дискретных выборок (рис. 38).

Рис. 38. Пример дискретизация времени: а – непрерывный сигнал; б – последовательность дискретных выборок

Если выборки осуществляются регулярно через интервал времени Т₀, то получается последовательность x_n(iT₀), где i=0, 1, 2,…,N-1. Общая длительность сигнала T=N×T₀.

Полагают, что функции x_n(iT₀) и S_n(RDf) связаны парой дискретного преобразования Фурье (ПДФ):

— прямого:

;

— и обратного:

.

При этом T₀Df=1/N.

Так же по аналогии с интегралом Фурье записывают дискретные преобразования в виде:

;

,

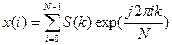где ;

x(i)=x_n(iT₀)- i-я выборка последовательности значений сигнала.

Это выражения часто используют при построении алгоритмов обработки дискретных сигналов.

Однако, вычисления, проводимые при выполнении ДПФ, довольно громоздки; они требуют примерно N² арифметических операций. Для ускорения преобразования разработаны специальные алгоритмы, значительно сокращающие объем и продолжительность вычислительных операций. Эти алгоритмы называют БПФ.

К спектральным характеристикам, используемым на практике, относятся также текущий и мгновенный спектры. Согласно выражению:

,

для каждого спектра сигнала x(t) необходимо выполнить интегрирование по времени в бесконечных пределах. Но реальные физические процессы обычно исследуются в течение конечного времени, и, следовательно, интегрирование ведется в пределах от момента начала наблюдения до данного, текущего момента t.

Тогда спектр примет вид:

.

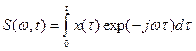Функция S(w, t) является функцией не только частоты, но и времени и называется текущим спектром.

Это понятие важно для теории и техники анализа спектра. Дело в том, что периодичность процесса проявляется лишь за достаточно большое время,– по крайней мере, за несколько периодов (рис. 39).

Рис. 39.

В течение же небольшой части периода характерные черты процесса вырисоваться не успевают. Спектр короткого отрезка процесса– сплошной, так как этот отрезок по существу является коротким импульсом (рис. 40). Переход к линейчатому спектру происходит лишь в пределе, когда t®µ (строго теоретически); на практике оказывается достаточной при условии t=nT (n>>1).

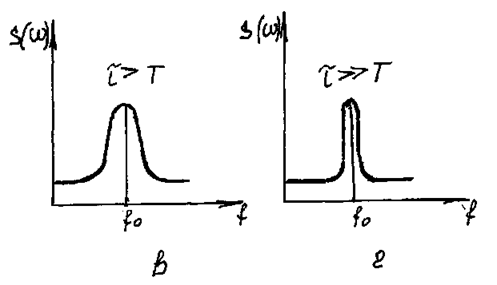
Рис. 40.

Мгновенный спектр описывается функцией:

,

и определяется как спектр отрезка сигнала длительностью Т, непосредственно предшествующего данному моменту t. В частности, мгновенный спектр нужно рассматривать как разность двух текущих спектров, то есть как приращение текущего спектра за интервал времени Т.

,

где S(w, t)- текущий спектр.

Спектральные характеристики случайных процессов

Как уже отмечалось ранее, случайным называется процесс x(t), мгновенные значения которого есть случайные величины. Изучение этих процессов есть сложный вопрос, требующий применения статистических методов анализа. При статистическом подходе отказываются от определения точного результата отдельного опыта, или измерения основываются на рассмотрении множества удается найти закономерности и количественные соотношения, характеризующие случайный процесс в среднем.

При измерениях случайный процесс проявляется в виде отдельных его реализаций. Полное представление процесса возможно с помощью так называемого ансамбля, то есть бесконечной совокупности реализаций. Ансамбль– математическая абстракция, модель случайного процесса (рис. 41). Конкретные реализации, наблюдаемые при эксперименте, представляют собой физические процессы, явления или объекты и входят в ансамбль как его неотъемлемая часть.

Наличие и отсутствие зависимости значений вероятностных характеристик от времени или номера реализации определяют стационарность и эргодичность.

Рис. 41. Ансамбль реализаций случайного процесса

Различают две основные группы характеристик случайных процессов, содержащие информацию:

1. о распределении значений процесса во времени (среднее значение, функция корреляции, функция распределения);

2. о распределении энергии процесса по частоте (спектральная плотность, полоса частот).

Истинные характеристики случайных процессов, определяемые в большинстве случаев как интегралы по бесконечным пределам, в принципе можно найти на основании бесконечно большого количества возможных реализаций процесса или в случае эргодичности– на основании одной реализации бесконечной длительности.

Реально можно наблюдать только ограниченные выборки, то есть реализацию конечной длительности или конечный ансамбль реализаций. Поэтому задача измерений состоит в том, чтобы найти оценки характеристик случайного процесса на основании конечной выборки. Эти оценки называются выборочными.

Рассмотрим более детально эти характеристики:

Спектральной характеристикой стационарных случайных процессов служит спектральная плотность мощности G_x(f) или S(w). Она выражает приходящуюся на единицу полосы частот среднюю мощность процесса (например, при исследовании случайного процесса изменения напряжения или тока, спектральная плотность характеризует мощность в полосе частот, выделяемую на резисторе в 1 Ом). Соотношение между спектральной плотностью стационарного случайного процесса x(t) и его корреляционной функцией R_x(t) дается парой преобразования Фурье:

;

.

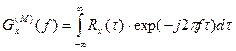Здесь спектральная плотность определена для положительных и отрицательных значений частоты, причем . Это представление используется для теоретического спектрального анализа.

При прикладных исследованиях и измерениях пользуются односторонней (физической) спектральной плотностью , отличной от нуля лишь при частотах f³0. Она определяется из следующих выражений:

;

.

Спектральная плотность мощности (спектр мощности) можно получить через текущий спектр реализаций:

,

где М- символ математического ожидания,

а также через мгновенный спектр l(f, t):

.

При теоретических и практических исследованиях часто используют нормированную спектральную плотность стационарного случайного процесса:

,

где 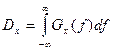– дисперсия процесса x(t) (площадь под кривой (рис. 42)).

Рис. 42.

Функция g_x(f) связана с нормированной корреляционной функцией r_x(t) выражением:

.

Измеряются данные характеристики в децибелах.

Полной характеристикой служит КЕПСТР, представляющий собой обратное преобразование Фурье натурального логарифма нормированного спектра g_x(f):

,

где g- переменная, имеющая размерность времени.

Следует отметить, что в отличии от спектрального анализа детерминированных сигналов спектральная плотность случайного процесса не дает возможности восстановить какую-либо реализацию сигнала, так как она является усредненной характеристикой и не содержит сведений о фазах отдельных спектральных составляющих. Можно указать несколько различных по характеру случайных сигналов, имеющих одинаковые спектральную плотность и корреляционную функцию. Поэтому они характеризуют случайный сигнал явно неполно.

Взаимная спектральная плотность стационарно связанных процессов x₁(t) и x₂(t) определяется через преобразование Фурье от взаимной корреляционной функции процессов:

.

Спектральная плотность мощности в общем виде есть четная функция частоты, то есть G(w)=G(-w) и для взаимной обработки нескольких случайных сигналов.

Как видно, в последних выражениях фигурирует автокорреляционная функция R_x(t), являющаяся частным представлением корреляционной функции, которая рассмотрена выше.

Оценку значений функции автокорреляции и взаимной корреляции случайных эргодических процессов осуществляют в соответствии с алгоритмом (рис. 43).

Рис. 43.

;

.

При этом, для правильности результата процессы должны быть заданы на интервале времени (T+t). В этом случае оценки по последним выражениям являются состоятельными и несмещенными.

Дисперсию оценки функции корреляции определяют как:

,

где .

Применение автокорреляционной функции очень важно для исследования свойств сигнала. Она, например, позволяет оценить степень случайности сигнала, периодичность, дисперсию, наличие постоянной составляющей и другие характеристики.

Сигнал в общем виде может быть представлен как сумма двух составляющих: детерминированной и случайной. При этом детерминированная состоит, например, из суммы простых гармоник, а случайная– функция с математическим ожиданием равным нулю, и дисперсией D:

,

где A, B- коэффициенты Фурье;

i- номер гармоники.

Автокорреляционная функция такого сигнала покажет степень зависимости сечений случайной функции, разделенных интервалом времени t. Автокорреляционная функция будет иметь вид:

,

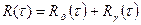где R_b(t)- автокорреляционная функция детерминированной составляющей;

R_g(t)- автокорреляционная функция случайной составляющей.

Это поясняется рис. 44.

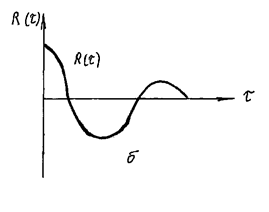
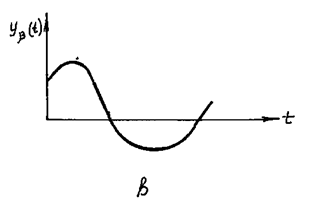
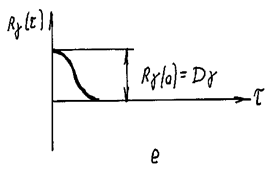
Рис. 44.

Отсюда следует, что коррелограмма сигнала, содержащего систематическую у_b(t) и случайную у_g(t) составляющие, в свою очередь состоит из коррелограммы систематической R_b(t) и коррелограммы случайной R_g(t) составляющих исследуемого сигнала.

В составе корреляционной функции систематической составляющей сигнала остаются те же гармоники, что и в сигнале, на амплитуды их изменяются. Так как амплитуды гармоник сигнала при расчете корреляционной функции возводятся в квадрат, то большие амплитуды увеличиваются в соответственно большее число раз, чем малые, то есть коррелограмма выделяет более мощные составляющие сигнала и затушевывает слабые.

Для рассматриваемого случая, то есть когда сигнал с детерминированной и случайной составляющей, рассчитанная по автокорреляционной функции спектральная плотность будет также выражаться через сумму спектральных плотностей систематической и случайной составляющих:

.

В качестве примера на рис. 45 показаны коррелограмма и спектрограмма сигнала. Спектрограмма имеет доминирующее значение для частоты w₁ соответствующей шагу периодической составляющей l, определенной с помощью коррелограммы.

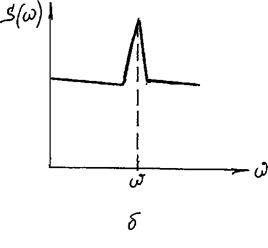
Рис. 45.

Анализ сигналов с помощью спектральной плотности отличается тем, что она отличается непрерывным спектром частот сигнала. В этом отношении спектральная плотность имеет существенное преимущество перед гармоническим анализом с помощью рядов Фурье, который дает дискретный спектр частот. Также, с помощью спектральной плотности можно выявить доминирующие составляющие сигнала и определить удельный вес любого интервала частот в дисперсии, равной площади под кривой спектра.

Дата добавления: 2014-01-06