Измерение параметров дискретной случайной величины

Измерение параметров случайных величин

Практически все измеряемые величины, а вернее их значения, являются случайными (например, скорость электрона, температура воздуха в конкретное время). По своей сути случайную величину измерить в принципе невозможно, так как значение величины есть случайное число. Измерению подвергают неслучайные параметры случайной величины. Сюда относят закон распределения вероятности и его характеристики, то есть моменты.

Пусть случайная величина Q имеет априорное распределение вероятности, представленное на рис. 70.

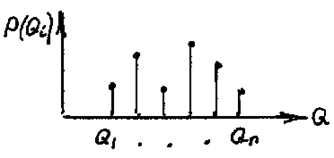
Рис. 70. Распределение вероятности случайной величины Q

Результат измерения значения величины, выполненного цифровым устройством, будет являться дискретным. При этом мы имеем некоторое иное распределение вероятности результатов.

Результаты обозначаем 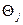. Значения Q₁, Q₂,…, Q_i- значения, которые может принимать величина.

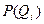- величина того, что величина примет значение Q_i.

При измерении прибор может выдавать результаты 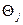. Значение 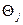определяется конструктивными особенностями (метрологическими характеристиками) прибора. 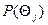- вероятность того, что показания прибора будут равны 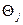(рис. 71)_. Данная вероятность зависит от 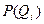(вероятности значений измеряемой величины), а также от помех– погрешностей преобразования, вызванных как внешними, так и внутренними факторами.

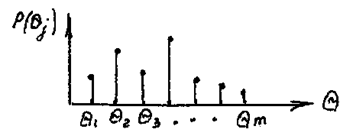
Рис. 71.

Поскольку показания прибора зависят от измеряемой величины Q_j, то в данном случае мы имеем две случайные величины взаимозависимые.

Если в конкретном измерении размер измеряемой величины будет Q_i, то вероятность получения результата 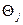будет определяться из выражения:

,

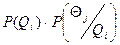где 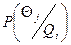- вероятность результата измерения 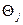при условии, что размер измеряемой величины равен Q_i (условия вероятности результата измерения );

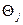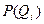- вероятность того, что размер величины равен Q_i.

По теории вероятности безусловная вероятность результата 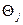равняется сумме условных вероятностей:

.

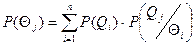То, что при вполне определенном размере измеряемой величины Q_i, результат измерения является неоднозначным и может иметь различные значения 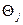, вероятность каждого из которых равна 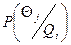свидетельствует о влиянии на процедуру измерения случайных факторов (помех) внешнего и внутреннего характера.

Значение безусловной вероятности 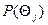характеризует вероятность того, что результат измерения будет равен 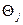независимо от того, какое из n- возможных значений примет измеряемая величина. При измерении случайной величины необходимо ответить на вопрос: как меняется в результате измерения априорное представление о распределении вероятности измеряемой величины.

Вероятность того, что при результате измерения 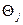измеряемая величина имела значение Q_i, определяется из выражения:

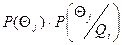, где

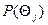- вероятность того, что показания будут ;

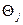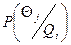- условная вероятность i-го размера измеряемой величины при показаниях .

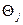Опуская промежуточные переходы получим, что вероятность:

.

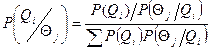Если измерению подвергается непрерывная измеряемая величина и для измерения применяют аналоговое средство, то распределение вероятностей заменяется на функцию плотности распределения:

.

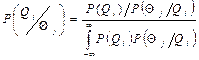Из выражений видно, что априорная информация о законе распределения вероятности измеряемой величины практически не играет роли, следовательно, информативность измерений очень велика.

Полученные выражения позволяют анализировать и распределение помехи.

Дата добавления: 2014-01-06