Помехи в связи

Лекция 6.

Определение. Помехой называется стороннее возмущение, мешающее правильному приему сигналов.

Если передается аналоговый или дискретный сигнал A(t), то на выходе канала связи в результате воздействия помех может быть принят сигнал:

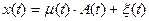(2.5.14)

где 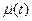-мультипликативная помеха;

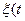) - аддитивная помеха.

Аддитивная помеха - не зависящее (не коррелированная с сигналом) от сигнала воздействие, вызванное сторонним возмущением поля, с помощью которого передается сигнал.

Мультипликативная помеха - обусловленная изменением коэффициента передачи канала связи под воздействием сторонних возмущений (пример: затирания при радиоприеме, другой пример: неудовлетворительно работающие АРУ и др.).

По происхождению помехи в канале разделяются на 2 большие группы: атмосферные и индустриальные.

Все помехи, независимо от их происхождения, по форме разделяются на импульсные, флуктуационые в виде периодических и синусоидальных колебаний.

Помеха называется импульсной, если она состоит из коротких импульсов, следующих друг за другом через промежутки времени, при которых нестационарный процесс от одного импульса успевает закончиться до появления следующего, т.е. если

τ<T_cp, T_cp - интервал между импульсами.

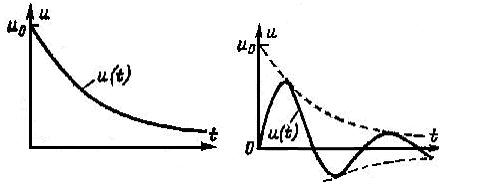
апериодическая помеха полупериодическая помеха

Рис. 2.5.2.

Апериодическая помеха описывается уравнением:

U(t)=о при t<0; (2.5.15)

U(t)=U₀e^-αt при ;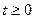

Полупериодические помехи:

U(t)=0 при t<0; (2.5.16)

U(t)=U₀e^-αt sinωt при ;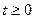

Апериодическая помеха возникает при воздействии короткого апериодическую RC или RL цепь, а полупериодические - при воздействии на колебательную цепь-RLC.

Флуктуационые помехи в отличие от импульсных имеют форму хаотически изменяющегося непрерывного колебания.

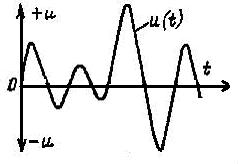
Рис. 2.5.3.

Для флуктуационных помех характерно отсутствие выбросов, отличающихся от среднего уровня больше, чем в 3 - 4 раза и справедливо соотношение: τ_u<<T_cp

При одних и тех же источниках на выходе устройства помехи могут быть импульсными или флуктуационными в зависимости от длительности нестационарного процесса τ_u,

Которая обратно пропорциональна полосе пропускания Δf данного устройства.

τ_u =k/ Δf (2.5.17)

Для простейших избирательных устройств .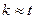

Известно, что для линейных устройств выходной уровень импульсных помех U_u пропорционален полосе пропускания Δt

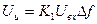(2.5.18)

при этом выходной уровень флуктуационной помехи будет

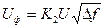(2.5.19)

где U_u-удельное напряжение помехи.

Рис. 2.5.4

В многоканальных системах тракты всех сигналов должны быть разделены, чтобы сигнал каждого источника информации мог попасть на свой приемник.

Пусть U_k(t) –сигналы датчиков, несущие некоторую информационную функцию x_k(t) и порождающие модуляцию параметров а_k носителя.

Тогда U_xk(t) –сигналы на выходах передающих устройств отдельных каналов.

В линии связи в этом случае действует суммарный сигнал U(t).

Тогда сигнал одного канала:

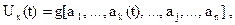(2.5.20)

здесь параметр 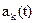передает информацию. А параметр 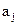или несколько параметров, характеризуют собственно индивидуальный канал. Каждому каналу соответствует определенное значение параметра 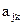или область значений 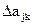параметра 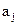. И тогда выражение (2.5.20) перепишется следующим образом

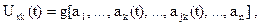(2.5.21(а))

или

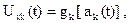(2.5.21(б))

В линию связи поступает составной сигнал:

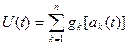(2.5.22)

Процесс разделения на приемной стороне можно рассматривать как фильтрацию, осуществляющую выделение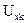

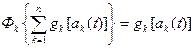(2.5.23)

В зависимости от вида оператора фильтрации 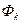различают следующие методы разделения сигналов: схемное разделение (пространственное), дифференциальное, частотное, временное фазовое, кодовое, по уровню, по форме, корреляционное.

Пространственное или разделение, когда каждому каналу отводится своя линия связи.

Дифференциальное разделение можно хорошо проиллюстрировать на примере телефонной линии.

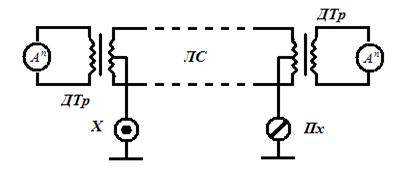
Рис 2.5.5

Здесь ДТр – дифференциальный трансформатор;

Х- датчик телемеханической информации;

Пх – приемник телемеханической информации.

Частотное разделение – это когда различных каналов водятся неперекрываемые полосы частотой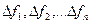

Спектры каналов 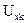складываются в соответствующую полосу частот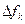

Определяется крайними частотами f_min полосы f₁ и f_max.

Низкочастотные сигналы U_k датчиков X_r модулируют по амплитуде или частоте высокочастотные сигналы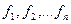

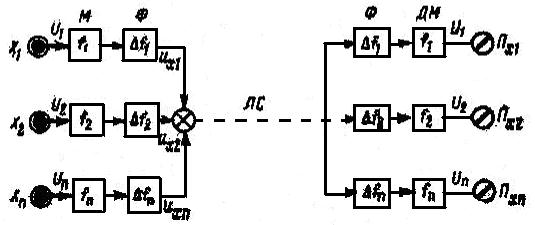
Рис. 2.5.6.

Сигналы на выходе модуляторов М имеют спектры 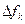, положение которых на шкале частот определяется несущими частотами 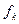, а ширина зависит от спектра сигналов датчиков.

Полосовые фильтры Ф передающей части служат для ограничения полосы частот каналов, т.е. разделения каналов.

На приемной стороне каждый Ф_к выделяет свой канал. На выходе демодулятора восстанавливается исходный канал датчика.

Временное разделение предусматривает передачу сигналов U_xk датчиков в определенные интервалы времени 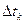. Разделение осуществляется специальными распределителями, работающими синхронно на передающей и приемной стороне.

Фазовое разделение применяют в двухканальной системе с синусоидальными сигналами, фазы которых различаются на 90⁰. Сигналы датчиков X_k модулируют амплитуду синусоидальных носителей, различающихся по фазе.

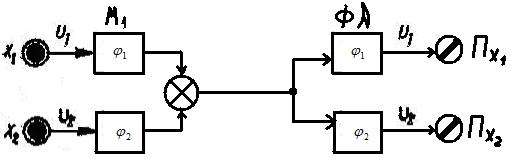
Рис. 2.5.7.

Сигналы U_xk на выходе модуляторов М имеют амплитуды, определяемые моделирующими функциями датчиков и фазы соответственно

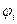и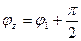

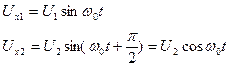(2.5.24)

Кодовое разделение. При кодовом разделении адрес нужного канала указывается кодированным сигналом, посылаемым в линию связи. Разделение на приемной стороне осуществляется декодирующим устройством, направляющим сообщения по выбранному каналу.

Разделение по уровню и по форме самостоятельно по Tутевичу гл.2; гл.4; гл.6 или Ильин гл.14-15.

Корреляционное разделение в последнее время получило широкое распространение. Действительно выражение 2.5.21(б) может быть представлено

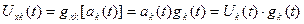(2.5.25)

Где функция 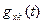описывает носитель с некоторой заданной величиной разделяющего параметра a_jk. Информационный параметр a_jk, модулирующий функцию 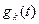по амплитуде, равен сигналу U_k(t) соответствующего датчика Х_к.

Этот параметр 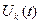, представляет собой функцию времени, медленно изменяющуюся по сравнению с 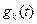, и его можно считать постоянным. Сигнал в линии связи в соответствии с выражением 2.5.22 представляет линейную комбинацию функций :

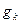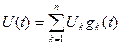(2.5.26)

Т.к. функции 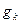линейно не зависимы, то они могут быть разделены линейными фильтрами. Такие многоканальные системы называются линейными.

Линейные системы на основе частотного, фазового, временного, по форме вида разделения каналов.

Линейность таких систем основана на ортогональности используемых сигналов (См. Гоноровский И.С. §2.15).

Т.е. используемый сигнал представляют как систему сигналов y_i(t_k) и y_j(t_k) таких, что

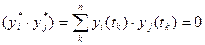(2.5.27)

Ортогональную систему образуют, например:

1) бесконечное множество функций 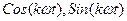, где k - целое неотрицательное число.

Такая система ортогональна на интервале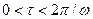

2) множество произвольных функций, определенных на непересекающихся интервалах времени т.к. при 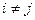они также образуют ортогональную систему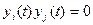

3) Множество, состоящее из дискретных знакопеременных функций на интервале 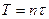, образующих коды Рида-Мюллера 1^го порядка

4) множество специальных функций: полиномы Лежандра, Чебышева, Якоби, Уолша и др.

Для ортогональных систем должно выполняться условие:

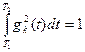(2.5.28)

при этом 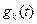- нормированная функция, т.е. исходную функцию 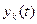умножают на нормирующий коэффициент:

(2.5.29)

Это позволяет представить сигнал, поступающий в линию в виде:

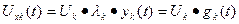(2.5.30)

где 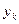(t) – исходная функция от датчика.

Для получения информационного параметра U_k нужно умножить принимаемый сигнал U(t) (см. выражение 2.5.26) на функцию 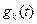и проинтегрировать в пределах T₁<t< T₂:

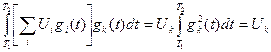(2.5.31)

(См. Корреляционный анализ, Гоноровский, гл.2)

Т.о. умножение принимаемого сигнала U(t) на соответствующую ортогональную функцию 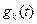позволяет разделить любые ортогональные сигналы или иначе происходит вычисление взаимокорреляционной функции сигналов u(t) и g_k (t).

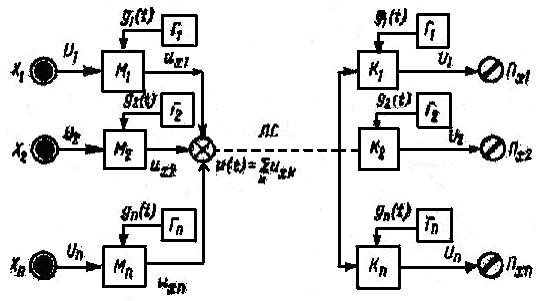
Рис. 2.5.7.

(назад в оглавление)

Дата добавления: 2014-01-06